Задание 3.84 - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 1. Страница 133
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
№3.84 учебника 2023-2024 (стр. 133):
№3.84 учебника 2021-2022 (стр. 133):
Найдите неизвестный член пропорции:
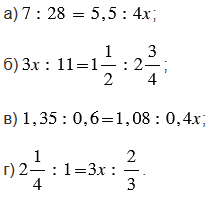
Подсказка
№3.84 учебника 2023-2024 (стр. 133):
№3.84 учебника 2021-2022 (стр. 133):
Вспомните:
- Что называют пропорцией.
- Что называют отношением.
- Что называют дробным выражением.
- Как найти неизвестный множитель.
- Умножение обыкновенных дробей, взаимно обратные числа.
- Деление десятичных дробей.
- Деление обыкновенных дробей.
- Сокращение дробей.
- Смешанные числа.
- Неправильные дроби.
Ответ
№3.84 учебника 2023-2024 (стр. 133):
№3.84 учебника 2021-2022 (стр. 133):
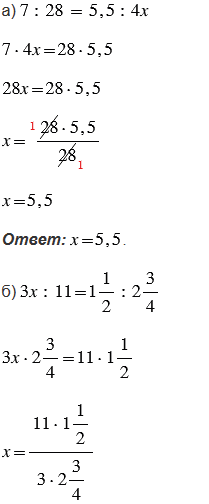
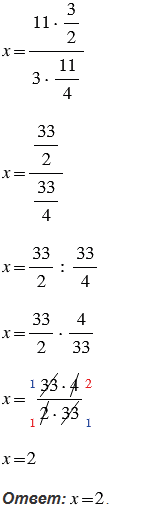
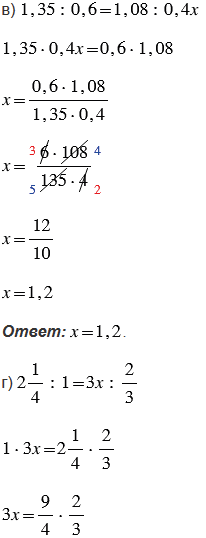
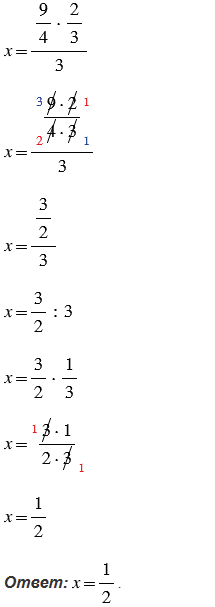
Пояснения:
Пропорция - это равенство двух отношений.
В пропорции 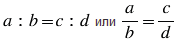 числа
числа 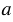 и
и 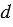 называют крайними членами, а числа
называют крайними членами, а числа 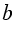 и
и 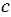 - средними членами пропорции.
- средними членами пропорции.
Чтобы найти неизвестный член пропорции, используем основное свойство пропорции:
Произведение крайних членов пропорции равно произведению ее средних членов: 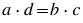 .
.
А затем находим неизвестный множитель по следующему правилу: чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
Если неизвестный член пропорции представляет собой дробное выражение, у которого в числителе и знаменателе стоят десятичные дроби, то переносим у десятичных дробей запятую вправо так, чтобы все числа стали натуральными, при этом количество знаков, на которые перенесена запятая в числителе и в знаменателе дробного выражения должно быть одинаковым, соответственно там, где знаков после запятой меньше, можно на конце дописывать нули, либо приписывать множители 10, 100, 1000, в зависимости от того на сколько знаков получилось меньше.
Произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель - произведению знаменателей.
Чтобы выполнить умножение смешанных чисел, нужно записать эти числа в виде неправильных дробей, а затем воспользоваться правилом умножения дробей. Чтобы преобразовать смешанное число в неправильную дробь, надо целую часть числа умножить на знаменатель дробной части и к полученному произведению прибавить числитель дробной части; эту сумму записать как числитель неправильной дроби, а в ее знаменатель записать знаменатель дробной части смешанного числа.
Чтобы найти частное двух дробей, надо делимое умножить на число, обратное делителю. При этом помним, обратным числу 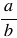 является число
является число 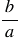 .
.
При выполнении умножения дробей, чтобы вычисления были проще, не надо перемножать сразу, лучше сделать это после сокращения. Сократить дробь - значит, разделить ее числитель и знаменатель на одно и то же число (наибольший общий делитель).
Также помним, что черту дроби можно заменить делением (числитель разделить на знаменатель).
Вернуться к содержанию учебника