Задание 190 - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№190 учебника 2013-2022 (стр. 56):
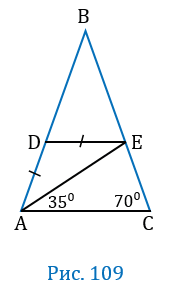
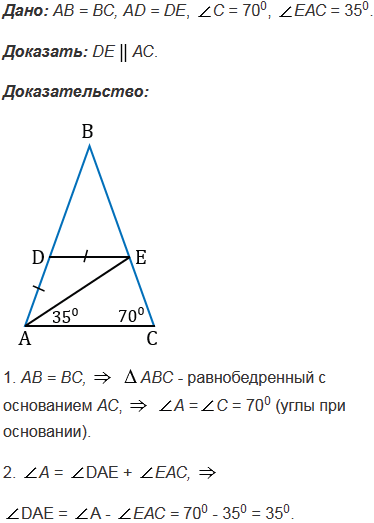
На рисунке 109 АВ = ВС, АD = DE, 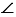 С = 700,
С = 700, 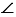 ЕАС = 350. Докажите, что DE
ЕАС = 350. Докажите, что DE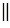 АС.
АС.
№190 учебника 2023-2024 (стр. 52):
С помощью циркуля и линейки разделите данный отрезок на четыре равные части.
Подсказка
№190 учебника 2013-2022 (стр. 56):
Вспомните:
- Какие прямые называются параллельными.
- Признаки параллельности двух прямых.
- Какой треугольник называется равнобедренным.
- Свойства равнобедренного треугольника.
№190 учебника 2023-2024 (стр. 52):
Ответ
№190 учебника 2013-2022 (стр. 56):


№190 учебника 2023-2024 (стр. 52):
Дано: отрезок АВ.
Разделить АВ на 4 равные части.
Решение:
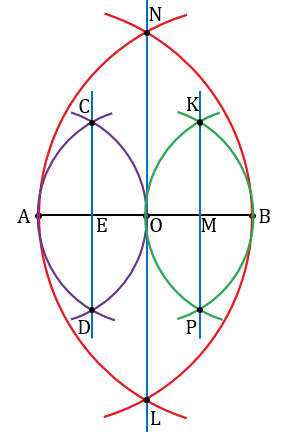
АЕ = ЕО = ОМ = МВ, т.к. Е и М - середины АО и ОВ, а О - середина АВ, т.е. АО = ОВ.
Пояснения:
Для того чтобы разделить отрезок на четыре равные части нужно разделить этот отрезок пополам, а потом каждую из половин разделить еще раз пополам.
Сначала с помощью линейки чертим произвольный отрезок АВ.
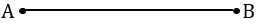
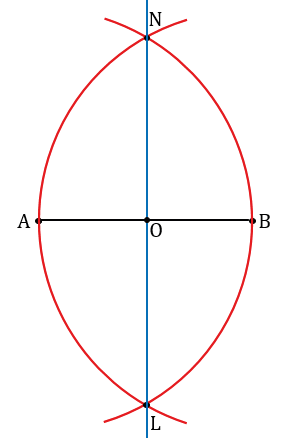
Построим с помощью циркуля середину отрезка АВ. Для этого строим две окружности (части окружностей, смотри выделенное красным) радиуса АВ с центрами в точках А и В, получим, что они пересекутся в двух точках, обозначим их N и L.
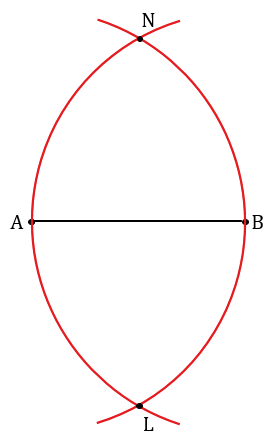
Далее проводим с помощью линейки прямую LN, она пересечет отрезок АВ в точке, обозначим ее буквой О. Точка О - середина отрезка АВ.
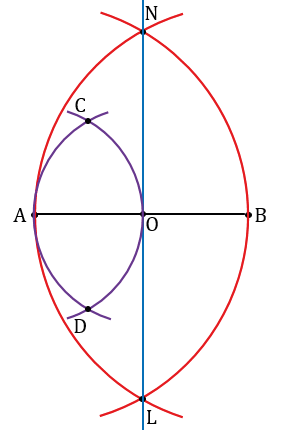
Теперь с помощью циркуля построим середину отрезка АО. Для этого строим две окружности (части окружностей, смотри выделенное фиолетовым) радиуса АО с центрами в точках А и О, получим, что они пересекутся в двух точках, обозначим их С и D.
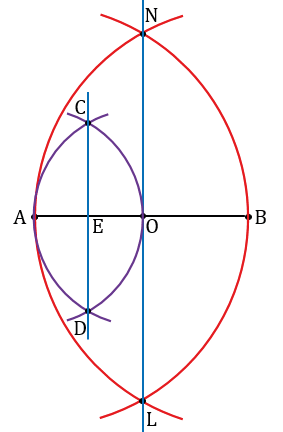
Далее проводим с помощью линейки прямую CD, она пересечет отрезок АO в точке, обозначим ее буквой E. Точка E - середина отрезка АO.
Теперь с помощью циркуля построим середину отрезка ОВ. Для этого строим две окружности (части окружностей, смотри выделенное зеленым) радиуса ОВ с центрами в точках В и О, получим, что они пересекутся в двух точках, обозначим их К и Р.
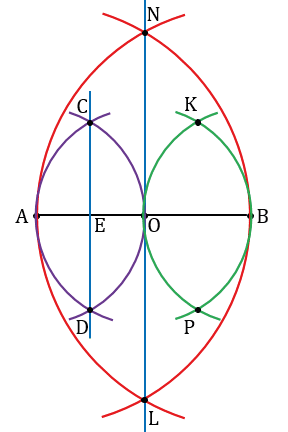
Далее проводим с помощью линейки прямую КР, она пересечет отрезок OВ в точке, обозначим ее буквой М. Точка М - середина отрезка OВ.
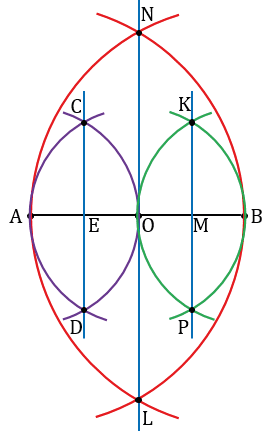
Докажем, что АЕ = ЕО = ОМ = МВ.
По построению точка О - середина отрезка АВ, тогда АО = ОВ, т.к. середина делит отрезок пополам (на два равных отрезка), при этом по построению точки Е и М середины отрезков АО и ОВ, значит АЕ = ЕО и ОМ = МВ, а т.к. равны сами отрезки АО и ОВ, то будут равны и их половины, т.е. АЕ = ЕО = ОМ = МВ.
Вернуться к содержанию учебника