Задание 186 - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№186 учебника 2013-2022 (стр. 56):
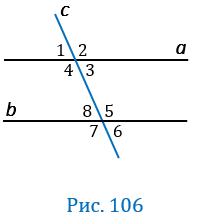
На рисунке 106 прямые 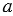 и
и 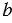 пересечены прямой
пересечены прямой 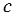 . Докажите, что
. Докажите, что 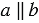 , если:
, если:
а) 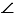 1=370,
1=370, 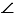 7 = 1430;
7 = 1430;
б) 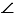 1=
1= 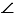 6;
6;
в)  1 = 450, а угол 7 в три раза больше угла 3.
1 = 450, а угол 7 в три раза больше угла 3.
№186 учебника 2023-2024 (стр. 52):
Постройте окружность данного радиуса, проходящую через две данные точки.
Подсказка
№186 учебника 2013-2022 (стр. 56):
Вспомните:
- Что такое прямая.
- Какие прямые называются параллельными.
- Какие углы образуются при пересечении двух прямых секущей.
- Признаки параллельности двух прямых.
- Какие углы называются смежными и их свойство.
- Какие углы называются вертикальными и их свойство.
№186 учебника 2023-2024 (стр. 52):
Вспомните:
- Что такое окружность, радиус окружности.
- Построения с помощью циркуля и линейки.
Ответ
№186 учебника 2013-2022 (стр. 56):
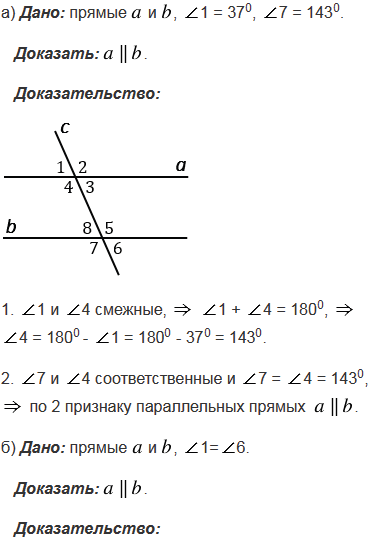





№186 учебника 2023-2024 (стр. 52):
Дано: R - радиус, точки А и В.
Построить: окружность радиуса R так, что А и В лежат на данной окружности.
Решение:
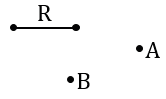
1 случай
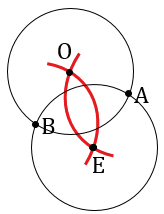
Ответ: 2 окружности с центрами в точках О и Е.
2 случай
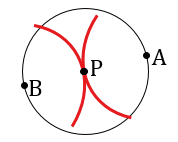
Ответ: 1 окружность с центром в точке Р.
3 случай

Ответ: нет решения.
Пояснения:
Данная задача имеет три случая решения, каждый из которых зависит от длины радиуса R и расположения точек А и В относительно друг друга.
1 случай
Начинаем с того, что с помощью циркуля и линейки строим две окружности (части окружностей, смотри выделенное красным) радиуса R с центрами в точках А и В. Для этого берем раствор циркуля равный длине радиуса R, далее ставим острие циркуля в точку А и чертим нужную нам часть окружности, затем также ставим острие циркуля в точку В и чертим нужную нам часть окружности. В данном случае точки А и В располагаются друг относительно друга так, что расстояние между ними меньше, чем 2R и окружности пересекутся в двух точках, обозначим их О и Е.
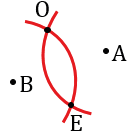
Далее строим окружности с центрами в точках О и Е радиуса R, при этом точки А и В будут лежать на этих окружностях, т.е. при АВ < 2R задача будет иметь два решения: окружность с центром в точке О и окружность с центром в точке Е.
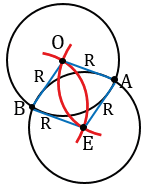
2 случай
Начинаем с того, что с помощью циркуля и линейки строим две окружности (части окружностей, смотри выделенное красным) радиуса R с центрами в точках А и В. Для этого берем раствор циркуля равный длине радиуса R, далее ставим острие циркуля в точку А и чертим нужную нам часть окружности, затем также ставим острие циркуля в точку В и чертим нужную нам часть окружности. В данном случае точки А и В располагаются друг относительно друга так, что расстояние между ними равно 2R и окружности пересекутся в одной точке, обозначим ее Р.
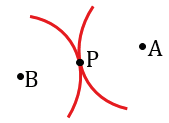
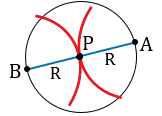
Далее строим окружность с центром в точке Р радиуса R, при этом точки А и В будут лежать на этой окружности, т.е. при АВ = 2R задача будет иметь одно решение: окружность с центром в точке Р.
3 случай
Начинаем с того, что с помощью циркуля и линейки строим две окружности (части окружностей, смотри выделенное красным) радиуса R с центрами в точках А и В. Для этого берем раствор циркуля равный длине радиуса R, далее ставим острие циркуля в точку А и чертим нужную нам часть окружности, затем также ставим острие циркуля в точку В и чертим нужную нам часть окружности. В данном случае точки А и В располагаются друг относительно друга так, что расстояние между ними больше, чем 2R и окружности не пересекутся.

Получаем, что при АВ > R невозможно построить окружность данного радиуса R так, чтобы точки А и В лежали на этой окружности, следовательно, в данном случае задача не имеет решения.
Вернуться к содержанию учебника