Задание 3. Вопросы для повторения к главе VI - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопросы для повторения к главе VI. Страница 133, 136
Вопрос
Выберите год учебника
№3 учебника 2013-2022 (стр. 133):
Какие многоугольники называются равновеликими и какие равносоставленными?
№3 учебника 2023-2024 (стр. 136):
Докажите, что сумма внешних углов выпуклого многоугольника, взятых по одному при каждой вершине, равна 3600.
Подсказка
№3 учебника 2013-2022 (стр. 133):
Вспомните:
- Что такое многоугольник.
- Что такое площадь многоугольника.
- Какие многоугольники называются равновеликими и какие равносоставленными.
№3 учебника 2023-2024 (стр. 136):
Ответ
№3 учебника 2013-2022 (стр. 133):
Равновеликие многоугольники - это многоугольники, которые имеют равные площади.
Равносоставленные многоугольники - это многоугольники, которые составлены из многоугольников, имеющих равные площади. На рисунке 3 изображены два равносоставленных многоугольника.
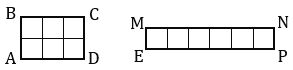
Любые два равносоставленных многоугольника равновеликие.
Верно и обратное утверждение: если два многоугольника равновеликие, то они равносоставленные (теорема Бойяи - Гервина).
№3 учебника 2023-2024 (стр. 136):
Внешний угол выпуклого многоугольника - угол, смежный с углом многоугольника. На рисунке ниже, угол OAB - внешний угол многоугольника АВСDE смежный с углом ВАЕ.
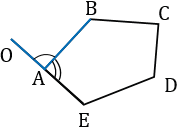
Сумма внешних углов выпуклого многоугольника равна 3600.
Дано: выпуклый многоугольник А1А2А3...Аn-1Аn.
Доказать: сумма внешних углов А1А2...Аn равна 3600.
Доказательство:
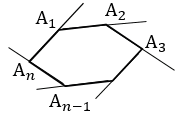
Если при каждой вершине выпуклого многоугольника А1А2...Аn взять по одному внешнему углу, то сумма этих внешних углов окажется равной
1800 - А1 + 1800 - А2 + ... + 1800 - Аn =
= n 1800 - (A1 + A2 + ... + An) =
1800 - (A1 + A2 + ... + An) =
= n 1800 - (n-2)
1800 - (n-2) 1800 =
1800 =
= n 1800 - n
1800 - n 1800 + 2
1800 + 2 1800 = 3600.
1800 = 3600.
Вернуться к содержанию учебника