Задание 255 - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№255 учебника 2013-2022 (стр. 79):
В равнобедренном треугольнике CDE с основанием CE проведена высота CF. Найдите 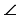 ECF, если
ECF, если 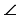 D = 540.
D = 540.
№255 учебника 2023-2024 (стр. 75):
Найдите сторону равнобедренного треугольника, если две другие стороны равны: а) 7 см и 3 см; б) 8 см и 2 см; в) 10 см и 5 см.
Подсказка
№255 учебника 2013-2022 (стр. 79):
Вспомните:
- Что такое треугольник.
- Что такое высота треугольника.
- Какой треугольник называется равнобедренным.
- Свойства равнобедренного треугольника.
- Какой треугольник называется прямоугольным.
- Свойства прямоугольного треугольника.
- Теорему о сумме углов треугольника.
№255 учебника 2023-2024 (стр. 75):
Вспомните:
- Какой треугольник называется равнобедренным.
- Неравенство треугольника.
Ответ
№255 учебника 2013-2022 (стр. 79):
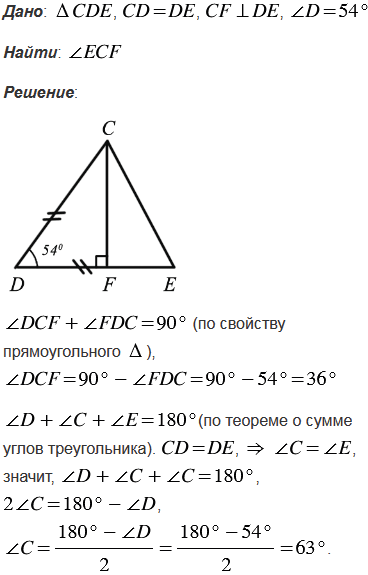


№255 учебника 2023-2024 (стр. 75):
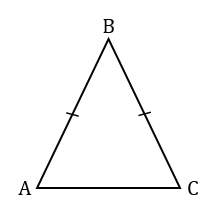
а) 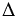 АВС - равнобедренный с основанием АС,
АВС - равнобедренный с основанием АС, 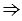 АВ = ВС.
АВ = ВС.
Если АС = 3 см, то АВ = ВС = 7 см, 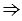 по тереме о неравенстве треугольника 3 < 7 + 7 и 7 < 3 + 7,
по тереме о неравенстве треугольника 3 < 7 + 7 и 7 < 3 + 7, 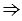 такой треугольник существует.
такой треугольник существует.
Если АС = 7 см, то АВ = ВС = 3 см, 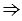 по тереме о неравенстве треугольника 3 < 7 + 3, а 7 > 3 + 3,
по тереме о неравенстве треугольника 3 < 7 + 3, а 7 > 3 + 3, 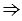 такой треугольник не существует.
такой треугольник не существует.
Ответ: 7 см.
б) 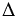 АВС - равнобедренный с основанием АС,
АВС - равнобедренный с основанием АС, 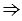 АВ = ВС.
АВ = ВС.
Если АС = 2 см, то АВ = ВС = 8 см,  по тереме о неравенстве треугольника 2 < 8 + 8 и 8 < 2 + 8,
по тереме о неравенстве треугольника 2 < 8 + 8 и 8 < 2 + 8,  такой треугольник существует.
такой треугольник существует.
Если АС = 8 см, то АВ = ВС = 2 см,  по тереме о неравенстве треугольника 2 < 8 + 2, а 8 > 2 + 2,
по тереме о неравенстве треугольника 2 < 8 + 2, а 8 > 2 + 2,  такой треугольник не существует.
такой треугольник не существует.
Ответ: 8 см.
в) 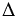 АВС - равнобедренный с основанием АС,
АВС - равнобедренный с основанием АС, 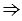 АВ = ВС.
АВ = ВС.
Если АС = 5 см, то АВ = ВС = 10 см, 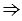 по тереме о неравенстве треугольника 5 < 10 + 10 и 10 < 5 + 10,
по тереме о неравенстве треугольника 5 < 10 + 10 и 10 < 5 + 10, 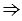 такой треугольник существует.
такой треугольник существует.
Если АС = 10 см, то АВ = ВС = 5 см, 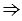 по тереме о неравенстве треугольника 5 < 10 + 5, а 10 = 5 + 5,
по тереме о неравенстве треугольника 5 < 10 + 5, а 10 = 5 + 5, 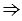 такой треугольник не существует.
такой треугольник не существует.
Ответ: 8 см.
Пояснения:
Равнобедренный треугольник - это треугольник, у которого равны две стороны. Тогда при решении данной задачи возможны два случая:
а) 1 случай
Предположим, что основание треугольника равно 3 см, тогда две другие стороны будут равны по 7 см. Теорема о неравенстве треугольника говорит о том, что каждая сторона треугольника меньше суммы двух других сторон. Проверим, выполняется ли эта теорема для данного случая.
3 < 7 + 7 и 7 < 3 + 7, оба условия соответствуют теореме, следовательно, такой треугольник существует. Значит третья сторона может быть равна 7 см.
2 случай
Предположим, что основание треугольника равно 7 см, тогда две другие стороны будут равны по 3 см. Теорема о неравенстве треугольника говорит о том, что каждая сторона треугольника меньше суммы двух других сторон. Проверим, выполняется ли эта теорема для данного случая.
3 < 7 + 3, а 7 > 3 + 3, первое условие соответствуют теореме, а второе - противоречит, т.к. получаем сторону большую, чем сумма двух других сторон, следовательно, такой треугольник не существует.
б) 1 случай
Предположим, что основание треугольника равно 2 см, тогда две другие стороны будут равны по 8 см. Теорема о неравенстве треугольника говорит о том, что каждая сторона треугольника меньше суммы двух других сторон. Проверим, выполняется ли эта теорема для данного случая.
2 < 8 + 8 и 8 < 2 + 8, оба условия соответствуют теореме, следовательно, такой треугольник существует. Значит третья сторона может быть равна равна 8 см.
2 случай
Предположим, что основание треугольника равно 8 см, тогда две другие стороны будут равны по 2 см. Теорема о неравенстве треугольника говорит о том, что каждая сторона треугольника меньше суммы двух других сторон. Проверим, выполняется ли эта теорема для данного случая.
2 < 8 + 2, а 8 > 2 + 2, первое условие соответствуют теореме, а второе - противоречит, т.к. получаем сторону большую, чем сумма двух других сторон, следовательно, такой треугольник не существует.
в) 1 случай
Предположим, что основание треугольника равно 5 см, тогда две другие стороны будут равны по 10 см. Теорема о неравенстве треугольника говорит о том, что каждая сторона треугольника меньше суммы двух других сторон. Проверим, выполняется ли эта теорема для данного случая.
5 < 10 + 10 и 10 < 5 + 10, оба условия соответствуют теореме, следовательно, такой треугольник существует. Значит третья сторона будет равна 10 см.
2 случай
Предположим, что основание треугольника равно 10 см, тогда две другие стороны будут равны по 5 см. Теорема о неравенстве треугольника говорит о том, что каждая сторона треугольника меньше суммы двух других сторон. Проверим, выполняется ли эта теорема для данного случая.
5 < 10 + 5, а 10 = 5 + 5, первое условие соответствуют теореме, а второе - противоречит, т.к. получаем сторону большую, чем сумма двух других сторон, следовательно, такой треугольник не существует.
Вернуться к содержанию учебника