Страница 87 - ГДЗ Математика 3 класс. Моро, Бантова. Учебник часть 1
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
Стр. 87 учебника 2023-2025:
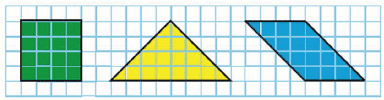
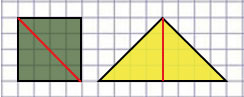
4. Начерти в тетради такие фигуры. Проведи в каждой фигуре один отрезок так, чтобы стало видно, что все три фигуры имеют одинаковые площади.
Стр. 87 учебника 2011-2022:
7. Реши уравнения.
75 + 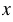 = 90 = 90 |
80 - k = 42 | 6 • n = 54 |
Подсказка
Стр. 87 учебника 2023-2025:
Вспомни, как вычислить площадь фигуры.
Стр. 87 учебника 2011-2022:
Решить уравнение – это значит найти такое значение неизвестного числа, при котором это равенство станет верным.
Ответ
Стр. 87 учебника 2023-2025:
Решение
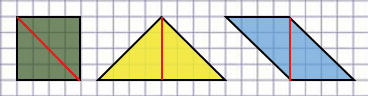
Пояснение
Каждая фигура составлена из двух одинаковых треугольников, поэтому данные три фигуры имеют одинаковые площади.
Ось симметрии фигуры - это прямая, которая делит фигуру на две симметричные части (если по этой прямой перегнуть фигуру, то ее части наложатся друг на друга).
Значит, проведенный отрезок будет осью симметрии у фигур 1 и 2.
Стр. 87 учебника 2011-2022:
Вариант ответа #1:


Вариант ответа #2:
Решение
|
75 + x = 90 x = 90 - 75 x = 15 |
80 - k = 42 k = 80 - 42 k = 38 |
6 • n = 54 n = 54 : 6 n = 9 |
Пояснение
Делаю проверку:
|
75 + x = 90 x = 90 - 75 x = 15 Проверка 75 + 15 = 90 90 = 90 |
80 - k = 42 k = 80 - 42 k = 38 Проверка 80 - 38 = 42 42 = 42 |
6 • n = 54 n = 54 : 6 n = 9 Проверка 6 • 9 = 54 54 = 54 |
Вопрос
Выберите год учебника
Стр. 87 учебника 2023-2025:
5. Поставь в кружки знаки арифметических действий так, чтобы равенства стали верными. Если надо, используй скобки.

8  4
4  2 = 34
2 = 34
8  4
4  2 = 10
2 = 10
8  4
4  2 = 4
2 = 4
8  4
4  2 = 14
2 = 14
8  4
4  2 = 1
2 = 1
8  4
4  2 = 30
2 = 30
8  4
4  2 = 48
2 = 48
8  4
4  2 = 64
2 = 64
Стр. 87 учебника 2011-2022:
8. 1) Найди площадь прямоугольника BCKE и площадь прямоугольника AEKD.
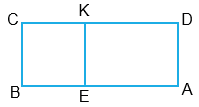
2) Найди двумя способами площадь прямоугольника ABCD.
Подсказка
Ответ
Стр. 87 учебника 2023-2025:
Вариант ответа #1:
Решение

Пояснение
|
8 • 4 + 2 = 34 1) 8 • 4 = 32 2) 32 + 2 =34 |
8 : 4 : 2 = 1 1) 8 : 4 = 2 2) 2 : 2 = 1 |
|
8 + 4 - 2 = 10 1) 8 + 4 = 12 2) 12 - 2 = 10 |
8 • 4 - 2 = 30 1) 8 • 4 = 32 2) 32 - 2 = 30 |
|
8 : 4 + 2 = 4 1) 8 : 4 = 2 2) 2 + 2 = 4 |
8 • (4 + 2) = 48 1) 4 + 2 = 6 2) 8 • 6 = 48 |
|
8 + 4 + 2 = 14 1) 8 + 4 = 12 2) 12 + 2 = 14 |
8 • (4 • 2) = 64 1) 4 • 2 = 8 2) 8 • 8 =64 |
Вариант ответа #2:
| 8 • 4 + 2 = 34 | 8 : 4 : 2 = 1 |
| 8 + 4 - 2 = 10 | 8 • 4 - 2 = 30 |
| 8 : 4 + 2 = 4 | 8 • (4 + 2) = 48 |
| 8 + 4 + 2 = 14 | 8 • (4 • 2) = 64 |
Пояснение
|
8 • 4 + 2 = 32 + 2 =34 |
8 : 4 : 2 = 2 : 2 = 1 |
|
8 + 4 - 2 = 12 - 2 = 10 |
8 • 4 - 2 = 32 - 2 =30 |
|
8 : 4 + 2 = 2 + 2 = 4 |
8 • (4 + 2) = 8 • 6 = 48 |
|
8 + 4 + 2 = 12 + 2 = 14 |
8 • (4 • 2) = 8 • 8 = 64 |
Стр. 87 учебника 2011-2022:
Вариант ответа #1:

Пояснение
С помощью линейки измеряем длину и ширину каждого из прямоугольников:
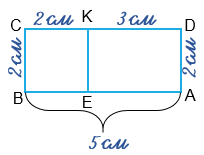
Задание 1:
Площадь BCKE:
BC · BE = 2 • 2 = 4 (см²)
Площадь AEKD:
KD · DA = 3 • 2 = 6 (см²)
Задание 2:
Площадь BCDA:
1 способ:
BC = 2 см
CD = 5 см
Площадь BCDA:
BC · CD = 2 • 5 = 10 (см²)
2 способ:
Складываю площади прямоугольников BCKE и AEKD, значит, площадь BCDA:
4 + 6 = 10 (см²)
Вариант ответа #2:
Задание 1
Площадь ВСКЕ:
ВС • ВЕ = 2 • 2 = 4 (см2)
Площадь АЕКD:
КD • DA = 3 • 2 = 6 (см2)
Задание 2
Площадь ВСDА:
1 способ:
Измеряю стороны прямоугольника ВСDА:
ВС = 2 см
СD = 5 см
Площадь ВСDА:
ВС • СD = 2 • 5 = 10 (см2)
2 способ:
Складываю площади прямоугольников ВСКЕ и АЕКD, значит, площадь ВСDА:
4 + 6 = 10 (см2)
Вопрос
Выберите год учебника
Стр. 87 учебника 2023-2025:
6. Вычислительная машина работает так:
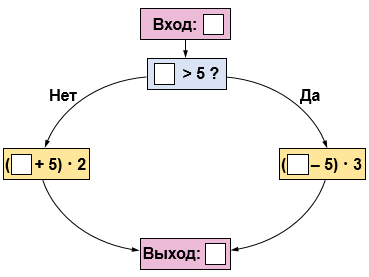
1) Какое число будет получаться на выходе из машины, если в неё ввести число: 3, 8, 2, 11, 14?
2) Какое число ввели в машину, если на выходе из машины получили число 3?
Стр. 87 учебника 2011-2022:
9. 1) Сделай такой же чертёж в тетради и подумай, как можно узнать площадь каждой из фигур с общей стороной OK (рис. 1); с общей стороной NP (рис. 2).
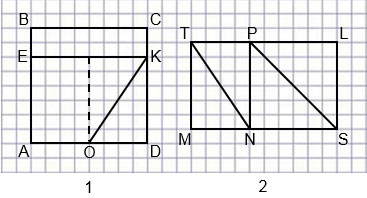
2) Узнай, площадь какой фигуры меньше: прямоугольника BCKE или треугольника OKD - и на сколько квадратных сантиметров.
Подсказка
Стр. 87 учебника 2023-2025:
Вспомни порядок выполнения действий при нахождении значения числовых выражений со скобками и без них.
Стр. 87 учебника 2011-2022:
Площадь прямоугольника равна произведению его длины и ширины.
Ответ
Стр. 87 учебника 2023-2025:
Вариант ответа #1:
Решение

Пояснение
Задание 1:
Обращаю внимание на синий прямоугольник:
1) если вводимое число больше 5, перехожу по стрелке ДА и выполняю действие:
(ЧИСЛО - 5) • 3
2) если вводимое число меньше 5, перехожу по стрелке НЕТ и выполняю действие:
(ЧИСЛО + 5) • 2
Задание 2:
Ввели 6, получили выражение
(6 - 5) • 3 = 1 • 3 = 3
Вариант ответа #2:
Задание 1:
3 ⇒ (3 + 5) • 2 ⇒16
8 ⇒ (8 - 5) • 3 ⇒ 9
2 ⇒ (2 + 5) • 2 ⇒ 14
11 ⇒ (11 - 5) • 3 ⇒ 18
14 ⇒ (14 - 5) • 3 ⇒ 27
Задание 2:
Ввели число 6.
Пояснение
Задание 1:
Обращаю внимание на синий прямоугольник:
1) если вводимое число больше 5, перехожу по стрелке ДА и выполняю действие:
(ЧИСЛО - 5) • 3
2) если вводимое число меньше 5, перехожу по стрелке НЕТ и выполняю действие:
(ЧИСЛО + 5) • 2
Задание 2:
Ввели 6, получили выражение
(6 - 5) • 3 = 1 • 3 = 3
Стр. 87 учебника 2011-2022:
Решение


Пояснение
Задание 1:
Фигуры с общей стороной OK: треугольник OKD и четырёхугольник ОКЕА.
Площадь треугольника OKD равна
(OD • KD) : 2 = (2 • 3) : 2 = 6 : 2 = 3 (см²)
Площадь четырехугольника ОКЕА равна разности площадей прямоугольника EKDA и треугольника OKD:
4 • 3 - 3 = 12 - 3 = 9 см²
Фигуры с общей стороной NP: треугольник NPS, квадрат NPLS, треугольник NPT и прямоугольник NPTM.
Площадь квадрата NPLS равна:
NP • LS = 3 • 3 = 9 см²
Площадь треугольника NPS в 2 раза меньше площади квадрата NPLS : 2 (мы ещё не умеем делить 9 на 2)
Площадь прямоугольника NPTM равна
NP • NM = 3 • 2 = 6 см²
Площадь треугольника NPT в 2 раза меньше площади прямоугольника NPTM, то есть площадь треугольника NPT равна:
6 : 2 = 3 см²
Задание 2:
Площадь прямоугольника ВСКЕ равна:
ВС • СК = 4 • 1 = 4 см²
Площадь треугольника OKD равна:
(OD • KD): 2 = (2 • 3) : 2 = 6 : 2 = 3 см²
Площадь OKD меньше площади ВСКЕ.
4 - 3 = 1 см²
Площадь OKD меньше площади ВСКЕ на 1 см².
Вопрос
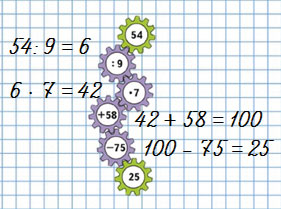
На сколько 9 меньше, чем 72?
Во сколько раз 6 меньше, чем 54?
Подсказка
Ответ
Вопрос
Цепочка:
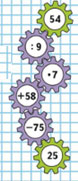
Подсказка
Вернуться к содержанию учебника