Упражнение 912 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№912 учебника 2023-2025 (стр. 205):
Изобразите на координатной прямой промежуток и назовите его:
а) \((3; 7)\);
б) \([1; 6]\);
в) \((-\infty; 5)\);
г) \([12; +\infty)\);
д) \((-\infty; 3]\);
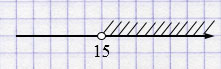
е) \((15; +\infty)\).
№912 учебника 2013-2022 (стр. 206):
Докажите, что если \(x+y+z=1\), то \[ \sqrt{4x+1}+\sqrt{4y+1}+\sqrt{4z+1}\le 5. \]
Подсказка
№912 учебника 2023-2025 (стр. 205):
Вспомните виды числовых промежутков.
№912 учебника 2013-2022 (стр. 206):
Вспомните:
- Доказательство неравенств.
- Арифметический квадратный корень.
- Свойства арифметического квадратного корня.
- Вынесение общего множителя за скобки.
- Сокращение дробей.
- Квадрат разности двух выражений.
Ответ
№912 учебника 2023-2025 (стр. 205):
а) \((3; 7)\) — интервал.
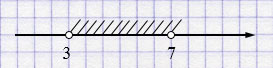
б) \([1; 6]\) — числовой отрезок.
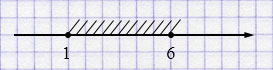
в) \((-\infty; 5)\) — открытый числовой луч.
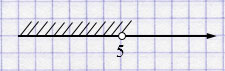
г) \([12; +\infty)\) — числовой луч.
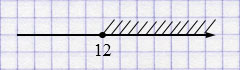
д) \((-\infty; 3]\) — числовой луч.
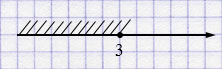
е) \((15; +\infty)\) — открытый числовой луч.
№912 учебника 2013-2022 (стр. 206):
Если \(x+y+z=1\), то
\( \sqrt{4x+1}+\sqrt{4y+1}+\sqrt{4z+1}\le 5. \)
\( \sqrt{4x+1}\le \frac{(4x+1)+1}{2}\)
\( \sqrt{4x+1}\le \frac{4x+2}{2}\)
\( \sqrt{4x+1}\le \frac{\cancel2(2x+1)}{\cancel2}\)
\( \sqrt{4x+1}\le2x+1\)
Аналогично,
\(\sqrt{4y+1}\le 2y+1\),
\(\sqrt{4z+1}\le 2z+1. \)
Складываем неравенства:
\( \sqrt{4x+1}+\sqrt{4y+1}+\sqrt{4z+1} \le (2x+1)+(2y+1)+(2z+1)\)
\( \sqrt{4x+1}+\sqrt{4y+1}+\sqrt{4z+1} \le (2x+2y+ 2z)+3\)
\(\sqrt{4x+1}+\sqrt{4y+1}+\sqrt{4z+1} \le2(x+y+z)+3\)
\(\sqrt{4x+1}+\sqrt{4y+1}+\sqrt{4z+1} \le2 \cdot 1+3\)
\(\sqrt{4x+1}+\sqrt{4y+1}+\sqrt{4z+1} \le5\)
Что и требовалось доказать.
Пояснения:
Использованное свойство:
для любого \(u\ge0\):
\( (\sqrt{u}-1)^2\ge0 \), то есть по формуле квадрата разности имеем:
\(u-2\sqrt{u}+1\ge0 \), откуда
\(2\sqrt{u}\le u+1 \), значит,
\(\sqrt{u}\le \frac{u+1}{2}. \)
Применили это свойство к каждому выражению \(4x+1,\;4y+1,\;4z+1\) и учли то, что \(x+y+z=1\).
Вернуться к содержанию учебника