Упражнение 223 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№223 учебника 2023-2025 (стр. 48):
Докажите, что выражение тождественно равно нулю:
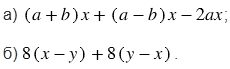
№223 учебника 2013-2022 (стр. 51):
Найдите значение выражения:
а) 5,9 • 2,6 + 5,9 • 3,2 + 5,8 • 4,1;
б) 6,8 • 8,4 - 1,6 • 8,4 + 5,2 • 1,6.
Подсказка
№223 учебника 2023-2025 (стр. 48):
Вспомните:
- Какие выражения называют тождественно равными.
- Подобные слагаемые.
- Противоположные числа.
№223 учебника 2013-2022 (стр. 51):
Вспомните:
- Распределительное свойство умножения.
- Сложение и вычитание десятичных дробей.
- Умножение десятичных дробей.
Ответ
№223 учебника 2023-2025 (стр. 48):
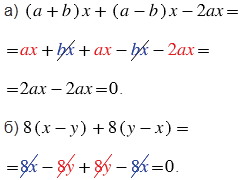
Пояснения:
Два выражения, значения которых равны при любых значениях переменных, называются тождественно равными.
При доказательстве мы использовали распределительное свойство умножения при раскрытии скобок, а именно умножали число, стоящее перед скобками на каждый компонент из скобок. Затем использовали то, что сумма противоположных выражений равна нулю (в решении противоположные слагаемые мы вычеркнули).
№223 учебника 2013-2022 (стр. 51):
а) 5,9 • 2,6 + 5,9 • 3,2 + 5,8 • 4,1 =
= 5,9 • (2,6 + 3,2) + 5,8 • 4,1 =
= 5,9 • 5,8 + 5,8 • 4,1 = 5,8 • (5,9 + 4,1) =
= 5,8 • 10 = 58.
б) 6,8 • 8,4 - 1,6 • 8,4 + 5,2 • 1,6 =
= 8,4 • (6,8 - 1,6) + 5,2 • 1,6 =
= 8,4 • 5,2 + 5,2 • 1,6 = 5,2 • (8,4 + 1,6) =
= 5,2 • 10 = 52.
Пояснения:
Чтобы найти значение выражения наиболее простым способом, используем распределительное свойство умножения, то есть выносим одинаковый множитель за скобки и сначала выполняем вычисления в скобках. В каждом выражении это свойство применяем дважды.
Вернуться к содержанию учебника