Упражнение 1060 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№1060 учебника 2023-2025 (стр. 205):
Разложите на множители:
а) \(1 + a - a^2 - a^3\);
б) \(8 - b^3 + 4b - 2b^2\).
№1060 учебника 2013-2022 (стр. 210):
Решите графически систему линейных уравнений:
а) \(\begin{cases} x - y = 1, \\ x + 3y = 9; \end{cases}\)
б) \(\begin{cases} x + 2y = 4, \\ -2x + 5y = 10; \end{cases}\)
в) \( \begin{cases} x + y = 0, \\ -3x + 4y = 14; \end{cases}\)
г) \(\begin{cases} 3x - 2y = 6, \\ 3x + 10y = -12. \end{cases} \)
Подсказка
№1060 учебника 2023-2025 (стр. 205):
№1060 учебника 2013-2022 (стр. 210):
Ответ
№1060 учебника 2023-2025 (стр. 205):
а) \(1 + a - a^2 - a^3 =\)
\(= (1 + a) - (a^2 + a^3) =\)
\( = (1 + a) - a^2(1 + a) =\)
\( = (1 + a)(1 - a^2)= \)
\(= (1 + a)(1 - a)(1 + a) =\)
\(= (1 + a)^2(1 - a). \)
Ответ: \((1 + a)^2(1 - a)\)
б) \(8 - b^3 + 4b - 2b^2=\)
\( =(8 + 4b) - (2b^2 + b^3) = \)
\( = 4(2 + b) - b^2(2 + b)= \)
\( = (2 + b)(4 - b^2) =\)
\(=(2 + b)(2 + b)(2 - b) =\)
\(= (2 + b)^2(2 - b) \)
Ответ: \((2 + b)^2(2 - b)\)
Пояснения:
а) Разложение выражения
\(1 + a - a^2 - a^3\):
Группируем так, чтобы можно было вынести общий множитель:
\( (1 + a) - (a^2 + a^3) =\)
\(=(1 + a) - a^2(1 + a) \)
Вынесем общий множитель \((1 + a)\):
\( (1 + a)(1 - a^2) \)
А затем применим формулу разности квадратов:
\( 1 - a^2 = (1 - a)(1 + a) =\)
\(= (1 + a)^2(1 - a) \)
б) Разложение выражения
\(8 - b^3 + 4b - 2b^2\):
Перегруппируем члены:
\( 8 + 4b - 2b^2 - b^3=\)
\(=(8 + 4b) - (2b^2 + b^3). \)
В первой группе выносим \(4\), во второй - \(b^2\):
\( 4(2 + b) - b^2(2 + b) =\)
\(=(2 + b)(4 - b^2). \)
Теперь применим формулу разности квадратов:
\( 4 - b^2 = (2 - b)(2 + b)=\)
\(= (2 + b)^2(2 - b) \)
№1060 учебника 2013-2022 (стр. 210):
а) \(\begin{cases} x - y = 1, \\ x + 3y = 9; \end{cases}\)
\( x - y = 1:\)
| \(x\) | 0 | 1 |
| \(y\) | -1 | 0 |
\( x + 3y = 9:\)
| \(x\) | 0 | 3 |
| \(y\) | 3 | 2 |

Ответ: \((3; 2).\)
б) \(\begin{cases} x + 2y = 4, \\ -2x + 5y = 10; \end{cases}\)
\( x + 2y = 4:\)
| \(x\) | 0 | 2 |
| \(y\) | 2 | 1 |
\(-2x + 5y = 10:\)
| \(x\) | 0 | -5 |
| \(y\) | 2 | 0 |

Ответ: \((0; 2).\)
в) \( \begin{cases} x + y = 0, \\ -3x + 4y = 14; \end{cases}\)
\(x + y = 0:\)
| \(x\) | 0 | -3 |
| \(y\) | 0 | 3 |
\(-3x + 4y = 14:\)
| \(x\) | 2 | -2 |
| \(y\) | 5 | 2 |

Ответ: \((-2; 2).\)
г) \(\begin{cases} 3x - 2y = 6, \\ 3x + 10y = -12. \end{cases} \)
\(3x - 2y = 6:\)
| \(x\) | 2 | 0 |
| \(y\) | 0 | -3 |
\(3x + 10y = -12:\)
| \(x\) | -4 | 1 |
| \(y\) | 0 | -1,5 |
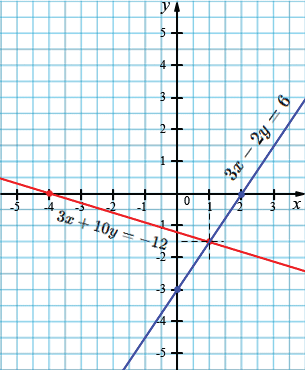
Ответ: \((1; -1,5).\)
Пояснения:
Решение системы графически означает построение двух прямых на координатной плоскости и нахождение их точки пересечения (если она существует).
Вернуться к содержанию учебника