Задание 6.79 - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 2. Страница 109

М(-6; 4), N(2; 3), K(1; -3), D(-7; 1)

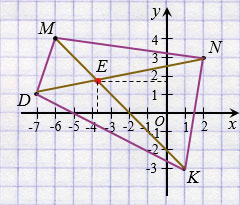
Е(-3,8; 1,8) - точка пересечения диагоналей МK и DN четырехугольника МNKD.

Пояснения:

Чертим прямоугольную систему координат с единичным отрезком 1 клетка.

Отметим в этой системе координат точки М(-6; 4), N(2; 3), K(1; -3), D(-7; 1).

Чтобы попасть в точку М с координатами (-6; 4), нужно сначала пройти по оси 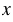от начала отсчета влево на 6 единиц, а потом - на 4 единицы вверх.

Чтобы попасть в точку N с координатами (2; 3), нужно сначала пройти по оси 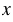от начала отсчета вправо на 2 единицы, а потом - на 3 единицы вверх.

Чтобы попасть в точку K с координатами (1; -3), нужно сначала пройти по оси 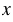от начала отсчета вправо на 1 единицу, а потом - на 3 единицы вниз.

Чтобы попасть в точку D с координатами (-7; 1), нужно сначала пройти по оси 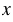от начала отсчета влево на 7 единиц, а потом - на 1 единицу вверх.

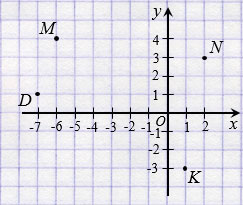
Далее последовательно соединяем точки М, N, K, D и получаем четырехугольник МNKD.

Теперь чертим диагонали МK и DN четырехугольника МNKD, которые пересекутся в точке Е. Чтобы определить координаты точки, нужно опустить из этой точки перпендикуляры на ос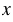и и 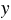, которые и укажут координаты точки.

Значит, точка Е имеет координаты

(-3,8; 1,8), т.е. Е(-3,8; 1,8).