Задание 6.21 - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 2. Страница 102
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
№6.21 учебника 2023-2024 (стр. 102):
Нарисуйте квадрат и проведите через каждую его вершину прямую, параллельную его диагонали. Обозначьте точки пересечения прямых буквами. Какой четырехугольник с вершинами в отмеченных точках получился?
Подсказка
№6.21 учебника 2023-2024 (стр. 102):
Вспомните:
- Что называют квадратом.
- Какие прямые называют параллельными.
Ответ
№6.21 учебника 2023-2024 (стр. 102):
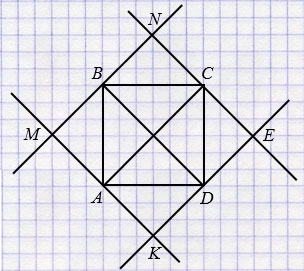
MN || AC, KE || AC, MK || BD, NE || BD.
Четырехугольник МNEK - квадрат.
Пояснения:
Две непересекающиеся прямые на плоскости называют параллельными.
Начертим произвольный квадрат АВСD и его диагонали АС и ВD.
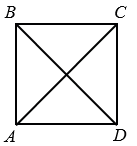
Проведем через вершину квадрата С, прямую параллельную диагонали ВD. Для этого прикладываем чертежный треугольник к диагонали АС одной из его сторон образующих прямой угол, а вдоль другой стороны чертежного треугольника, образующей прямой угол, прикладываем линейку.
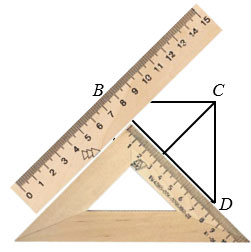
Далее, не меняя положения линейки, двигаем вдоль нее чертежный треугольник до вершины С и проводим вдоль его стороны через точку С прямую.

Прямая проведенная через вершину С будет параллельна диагонали ВD.
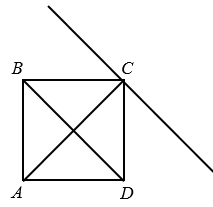
Аналогично через вершину А проводим прямую параллельную диагонали ВD, а через вершины В и D проводим прямые параллельные диагонали АС. Тоочки пересечения этих прямых обозначаем буквами М, N, Е и K.
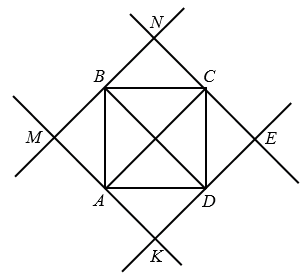
MN || AC, KE || AC, MK || BD, NE || BD.
Четырехугольник МNEK - квадрат.
Вернуться к содержанию учебника