Задание 6.371 - ГДЗ Математика 5 класс. Виленкин, Жохов. Учебник часть 2
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№6.371 учебника 2023-2024 (стр. 142):
Со склада в торговый зал магазина было отправлено 90,6 кг картофеля, что составило 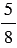 всего картофеля, имеющегося на складе. Сколько картофеля осталось на складе?
всего картофеля, имеющегося на складе. Сколько картофеля осталось на складе?
№6.371 учебника 2021-2022 (стр. 127):
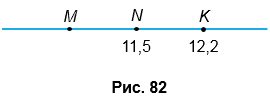
На рисунке 82 отрезки MN и NK равны. Найдите координату точки М. Найдите среднее арифметическое координат точек М и K.
Подсказка
№6.371 учебника 2023-2024 (стр. 142):
Вспомните:
- Обыкновенные дроби.
- Деление десятичных дробей.
- Умножение десятичных дробей.
- Вычитание десятичных дробей.
№6.371 учебника 2021-2022 (стр. 127):
Вспомните:
- Что называют средним арифметическим.
- Что называют координатным лучом.
- Деление десятичных дробей.
- Сложение и вычитание десятичных дробей.
Ответ
№6.371 учебника 2023-2024 (стр. 142):
1) 90,6 : 5 • 8 = 18,12 • 8 = 144,96 (кг) - картофеля было на складе.
|
|
2) 144,96 - 90,6 = 54,36 (кг)
| • | ||||||
| - | 1 | 4 | 4 | , | 9 | 6 |
| 9 | 0 | , | 6 | 0 | ||
| 5 | 4 | , | 3 | 6 |
Ответ: 54,36 кг картофеля осталось на складе.
Пояснения:
Знаменатель дроби (нижнее число) показывает на сколько равных частей разделили целое, а числитель дроби (верхнее число) - сколько таких частей взяли.
Со склада в торговый зал магазина было отправлено 90,6 кг картофеля, что составило 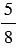 всего картофеля, имеющегося на складе. Знаменатель дроби
всего картофеля, имеющегося на складе. Знаменатель дроби 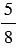 показывает, что весь картофель, имеющийся на складе, разделили на 8 равных частей, а числитель то, что взяли 5 таких частей, которые составили картофель, отправленный со склада в торговый зал магазина, то есть 90,6 кг, значит, всего на складе было:
показывает, что весь картофель, имеющийся на складе, разделили на 8 равных частей, а числитель то, что взяли 5 таких частей, которые составили картофель, отправленный со склада в торговый зал магазина, то есть 90,6 кг, значит, всего на складе было:
90,6 : 5 • 8 = 18,12 • 8 = 144,96 (кг).
Всего на складе было 144,96 кг картофеля, из которых 90,6 кг отправили в торговый зал магазина, значит, на складе осталось:
144,96 - 90,6 = 54,36 (кг).
Правила вычислений с десятичными дробями смотрите в подсказке.
№6.371 учебника 2021-2022 (стр. 127):
N(11,5), K(12,2), МN = NK,
М(?).
1) МN = NK = 12,2 - 11,5 = 0,7.
2) 11,5 - 0,7=10,8 - координата точки М.
3) (10,8 + 12,2) : 2 = 11,5
|
|
Ответ: М(10,8), среднее арифметическое координат точек М и K равно 11,5.
Пояснения:
Чтобы найти расстояние между точками на координатном луче, нужно из большей координаты вычесть меньшую координату.
N(11,5) и K(12,2), значит, расстояние между точками N и K, то есть
NK = 12,2 - 11,5 = 0,7.
Учитывая то, что по условию отрезки MN и NK равны, имеем МN = NK = 0,7.
Нам известно, что N(11,5) и МN = 0,7, тогда, чтобы найти координату точки М, нужно из координаты точки N вычесть длину отрезка МN, следовательно, координата точки М равна:
11,5 - 0,7 = 10,8.
Средним арифметическим ряда чисел называется частное от деления суммы этих чисел на количество слагаемых. Тогда для координат точек М и K среднее арифметическое будет равно 11,5 (координата точки N), так как:
(10,8 + 12,2) : 2 = 11,5.
Правила вычислений с десятичными дробями смотрите в подсказке.
Вернуться к содержанию учебника