Задание 6.315 - ГДЗ Математика 5 класс. Виленкин, Жохов. Учебник часть 2
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№6.315 учебника 2023-2024 (стр. 135):
Вычислите:
а) 0,42 • 10;
б) 0,33 • 100;
в) 0,14 + 0,12;
г) 22 • 0,22;
д) 1,72 • 100;
е) 0,42 + 0,82 - 0,23.
№6.315 учебника 2021-2022 (стр. 121):
Выполните деление и проверку умножением:
а) 0,6 : 0,5;
б) 9,28 : 2,9;
в) 19,035 : 0,81.
Подсказка
№6.315 учебника 2023-2024 (стр. 135):
№6.315 учебника 2021-2022 (стр. 121):
Ответ
№6.315 учебника 2023-2024 (стр. 135):
а) 0,42 • 10 = 0,4 • 0,4 • 10 =
= 0,16 • 10 = 1,6;
б) 0,33 • 100 = 0,3 • 0,3 • 0,3 • 100 =
= 0,09 • 0,3 • 100 = 0,027 • 100 = 2,7;
в) 0,14 + 0,12 = 0,1•0,1•0,1•0,1+0,1•0,1 =
= 0,0001 + 0,01 = 0,0101;
г) 22 • 0,22 = (2 • 2) • (0,2 • 0,2) =
= 4 • 0,04 = 0,16;
д) 1,72 • 100 = 1,7 • 1,7 • 100 =
= 2,89 • 100 = 289;
| × | 1 | 7 | |
| 1 | 7 | ||
| + | 1 | 1 | 9 |
| 1 | 7 | ||
| 2 | 8 | 9 |
е) 0,42 + 0,82 - 0,23 =
= 0,4 • 0,4 + 0,8 • 0,8 - 0,2 • 0,2 • 02 =
= 0,16 + 0,64 - 0,008 = 0,792.
|
|
Пояснения:
Степенью числа "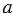
" с натуральным показателем "
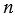", большим 1, называется произведение "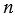" одинаковых множителей, каждый из которых равен числу "".
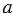Чтобы найти сумму (разность) десятичных дробей столбиком, нужно:
1) записать их друг под другом так, чтобы запятая была записана под запятой;
2) уравнять в них количество знаков после запятой;
3) выполнить сложение (вычитание), не обращая внимания на запятую;
4) в результате поставить запятую под запятой.
Чтобы найти произведение двух десятичных дробей, можно:
1) перемножить их, не обращая внимания на запятые;
2) в полученном произведении отделить запятой справа столько цифр, сколько их было после запятой в обоих множителях вместе.
№6.315 учебника 2021-2022 (стр. 121):
а) 0,6 : 0,5 = 6 : 5 = 1,2
|
Проверка: 1,2 • 0,5 = 0,6
|
б) 9,28 : 2,9 =92.8 : 29 = 3,2
|
Проверка: 3,2 • 2,9 = 9,28
|
в) 19,035 : 0,81 = 1903,5 : 81 = 23,5
| - | 1 | 9 | 0 | 3 | 5 | 8 | 1 | |||||||||||||
| 1 | 6 | 2 | 2 | 3 | 5 | |||||||||||||||
| - | 2 | 8 | 3 | |||||||||||||||||
| 2 | 4 | 3 | ||||||||||||||||||
| - | 4 | 0 | 5 | |||||||||||||||||
| 4 | 0 | 5 | ||||||||||||||||||
| 0 |
Проверка:
23,5 • 0,81 = 19,035
| × | 2 | 3 | 5 | ||
| 0 | 8 | 1 | |||
| + | 2 | 3 | 5 | ||
| 1 | 8 | 8 | 0 | ||
| 1 | 9 | 0 | 3 | 5 |
Пояснения:
Чтобы разделить десятичную дробь на десятичную, нужно:
1) перенести в делимом и делителе запятые вправо на столько цифр, сколько их содержится после запятой в делителе;
2) выполнить деление на натуральное число, а именно: разделить дробь на это число, не обращая внимания на запятую; поставить в частном запятую, когда кончится деление целой части.
Чтобы проверить деление умножением, нужно полученное частное умножить на делитель и если при умножении получится число, равное делимому, то деление выполнено верно.
Чтобы перемножить две десятичные дроби, надо:
1) записать дроби в столбик, как два натуральных числа не обращая внимание на запятые;
2) умножить их как натуральные числа, не обращая внимание на запятые;
3) в полученном произведении отделить запятой справа столько цифр, сколько их стоит после запятых в обоих множителях вместе.
Также учитываем то, что:
- если к десятичной дроби приписать справа какое угодно количество нулей, то получится дробь равная данной;
- если в десятичной дроби последние цифры - нули, то, отбросив их, получим дробь, равную данной;
- любое натуральное число можно представить в виде десятичной дроби с каким угодно количеством нулей после запятой.
Вернуться к содержанию учебника