Задание 6.197 - ГДЗ Математика 5 класс. Виленкин, Жохов. Учебник часть 2
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№6.197 учебника 2023-2024 (стр. 121):
Решите уравнение:
1) 4,4 + 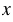 - 1,4 = 9,76;
- 1,4 = 9,76;
2) 10,3 - 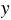 - 2,7 = 6,48.
- 2,7 = 6,48.
№6.197 учебника 2021-2022 (стр. 105):
Решите уравнение:
1) 4,4 + 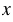 - 31,4 = 9,76;
- 31,4 = 9,76;
2) 10,3 - 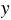 - 2,7 = 6,48.
- 2,7 = 6,48.
Подсказка
№6.197 учебника 2023-2024 (стр. 121):
№6.197 учебника 2021-2022 (стр. 105):
Вспомните:
- Что называют уравнением, его корни.
- Сложение и вычитание десятичных дробей.
- Свойства вычитания.
Ответ
№6.197 учебника 2023-2024 (стр. 121):


№6.197 учебника 2021-2022 (стр. 105):
1) 4,4 +  - 31,4 = 9,76
- 31,4 = 9,76
(4,4 +  ) - 31,4 = 9,76
) - 31,4 = 9,76
4,4 +  = 9,76 + 31,4
= 9,76 + 31,4
4,4 +  = 41,16
= 41,16
 = 41,16 - 4,4
= 41,16 - 4,4
 = 36,76
= 36,76
|
|
Ответ:  = 36,76.
= 36,76.
2) 10,3 - 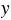 - 2,7 = 6,48
- 2,7 = 6,48
10,3 - (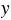 + 2,7) = 6,48
+ 2,7) = 6,48
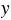 + 2,7 = 10,3 - 6,48
+ 2,7 = 10,3 - 6,48
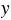 + 2,7 = 3,82
+ 2,7 = 3,82
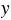 = 3,82 - 2,7
= 3,82 - 2,7
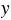 = 1,12
= 1,12
|
|
Ответ: 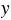 = 1,12.
= 1,12.
Пояснения:
1) В левой части уравнения
4,4 +  - 31,4 = 9,76
- 31,4 = 9,76
сначала применяем свойство вычитания числа из суммы, тогда уравнение можно записать так:
(4,4 +  ) - 31,4 = 9,76.
) - 31,4 = 9,76.
Теперь решаем уравнение относительно вычитания, то есть находим неизвестное уменьшаемое. Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое, тогда:
4,4 +  = 9,76 + 31,4.
= 9,76 + 31,4.
4,4 +  = 41,16.
= 41,16.
Далее решаем уравнение относительно сложения, то есть находим неизвестное слагаемое. Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое, тогда:
 = 41,16 - 4,4,
= 41,16 - 4,4,
 = 36,76.
= 36,76.
2) В левой части уравнения
10,3 - 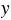 - 2,7 = 6,48
- 2,7 = 6,48
сначала применяем свойство вычитания суммы из числа, тогда уравнение можно записать так:
10,3 - (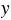 + 2,7) = 6,48.
+ 2,7) = 6,48.
Теперь решаем уравнение относительно вычитания, то есть находим неизвестное вычитаемое. Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность, тогда:
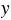 + 2,7 = 10,3 - 6,48,
+ 2,7 = 10,3 - 6,48,
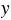 + 2,7 = 3,82.
+ 2,7 = 3,82.
Далее решаем уравнение относительно сложения, то есть находим неизвестное слагаемое. Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое, тогда:
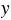 = 3,82 - 2,7,
= 3,82 - 2,7,
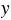 = 1,12.
= 1,12.
Вернуться к содержанию учебника