Задание 6.196 - ГДЗ Математика 5 класс. Виленкин, Жохов. Учебник часть 2
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№6.196 учебника 2023-2024 (стр. 121):
Два велосипедиста выехали из одного пункта одновременно в одном направлении. Скорость одного из них равна 27 км/ч, что на 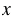 км/ч больше скорости другого. Какое расстояние будет между велосипедистами через 3 ч?
км/ч больше скорости другого. Какое расстояние будет между велосипедистами через 3 ч?
б) Составьте выражение для решения задачи и найдите его значение при 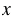 = 13; 17; 22.
= 13; 17; 22.
в) Есть ли в задаче лишнее условие?
№6.196 учебника 2021-2022 (стр. 105):
Два велосипедиста выехали из одного пункта одновременно в одном направлении. Скорость одного из них равна 27 км/ч, что на  км/ч больше, чем скорость другого.
км/ч больше, чем скорость другого.
а) Какое расстояние будет между велосипедистами через 3 ч?
б) Составьте выражение и найдите его значение при  = 13; 17; 22.
= 13; 17; 22.
в) Какое данное в условии задачи ли лишнее?
Подсказка
№6.196 учебника 2023-2024 (стр. 121):
№6.196 учебника 2021-2022 (стр. 105):
Вспомните:
- Задачи на движение.
- Числовые и буквенные выражения.
- Свойства вычитания.
- Умножение чисел.
Ответ
№6.196 учебника 2023-2024 (стр. 121):
27 км/ч - скорость первого велосипедиста,
(27 - 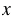 ) км/ч - скорость второго велосипедиста.
) км/ч - скорость второго велосипедиста.
27 - (27 - 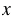 ) = 27 - 27 +
) = 27 - 27 + 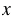 =
= 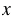 (км/ч) - скорость удаления.
(км/ч) - скорость удаления.
3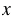 (км) - будет между велосипедистами через 3 ч.
(км) - будет между велосипедистами через 3 ч.
а) Если 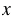 = 13, то
= 13, то
3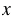 = 3 • 13 = 39 (км).
= 3 • 13 = 39 (км).
Если 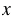 = 17, то
= 17, то
3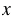 = 3 • 17 = 51 (км).
= 3 • 17 = 51 (км).
Если 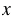 = 22, то
= 22, то
3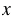 = 3 • 22 = 66 (км).
= 3 • 22 = 66 (км).
б) Лишнее данное в условии - скорость первого велосипедиста.
Ответ: а) 3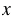 км; б) 39 км; 51 км; 66 км; в) а задаче есть лишнее условие - скорость первого велосипедиста.
км; б) 39 км; 51 км; 66 км; в) а задаче есть лишнее условие - скорость первого велосипедиста.
Пояснения:
Чтобы найти скорость удаления объектов, движущихся в одном направлении, нужно из большей скорости вычесть меньшую скорость.
По условию скорость первого велосипедиста 27 км/ч, что на 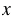 км/ч больше, чем скорость второго, значит, скорость второго велосипедиста равна (27 -
км/ч больше, чем скорость второго, значит, скорость второго велосипедиста равна (27 - 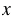 ) км/ч. Велосипедисты движутся в одном направлении, тогда скорость их удаления:
) км/ч. Велосипедисты движутся в одном направлении, тогда скорость их удаления:
27 - (27 - 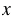 ) = 27 - 27 +
) = 27 - 27 + 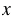 =
= 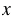 (км/ч).
(км/ч).
Чтобы найти расстояние, нужно время умножить на скорость движения.
Велосипедисты сближаются со скоростью 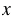 км/ч, тогда, учитывая то, что велосипедисты выехали одновременно из одного пункта, через 3 ч расстояние между ними станет равным: 3
км/ч, тогда, учитывая то, что велосипедисты выехали одновременно из одного пункта, через 3 ч расстояние между ними станет равным: 3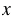 (км).
(км).
а) Чтобы найти значение буквенного выражения при заданном значении переменной, нужно в это выражение вместо буквы подставить числа, ей соответствующие, и выполнить вычисления (смотри решение).
б) Лишнее данное в условии - скорость первого велосипедиста, так как в ходе преобразований выражения для скорости удаления, скорость первого велосипедиста (27 км/ч) уходит и на дальнейшие результаты при решении задачи никак не влияет.
№6.196 учебника 2021-2022 (стр. 105):
27 км/ч - скорость первого велосипедиста,
(27 - 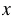 ) км/ч - скорость второго велосипедиста.
) км/ч - скорость второго велосипедиста.
27 - (27 - 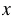 ) = 27 - 27 +
) = 27 - 27 + 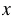 =
= 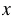 (км/ч) - скорость удаления.
(км/ч) - скорость удаления.
а) 3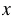 (км) - будет между велосипедистами через 3 ч.
(км) - будет между велосипедистами через 3 ч.
б) Если 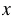 = 13, то
= 13, то
3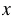 = 3 • 13 = 39 (км).
= 3 • 13 = 39 (км).
Если 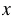 = 17, то
= 17, то
3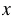 = 3 • 17 = 51 (км).
= 3 • 17 = 51 (км).
Если 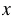 = 22, то
= 22, то
3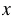 = 3 • 22 = 66 (км).
= 3 • 22 = 66 (км).
в) Лишнее данное в условии - скорость первого велосипедиста.
Ответ: а) 3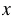 км; б) 39 км; 51 км; 66 км; в) скорость первого велосипедиста.
км; б) 39 км; 51 км; 66 км; в) скорость первого велосипедиста.
Пояснения:
Чтобы найти скорость удаления объектов, движущихся в одном направлении, нужно из большей скорости вычесть меньшую скорость.
По условию скорость первого велосипедиста 27 км/ч, что на 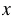 км/ч больше, чем скорость второго, значит, скорость второго велосипедиста равна (27 - ) км/ч. Велосипедисты движутся в одном направлении, тогда скорость их удаления:
км/ч больше, чем скорость второго, значит, скорость второго велосипедиста равна (27 - ) км/ч. Велосипедисты движутся в одном направлении, тогда скорость их удаления:
27 - (27 - 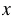 ) = 27 - 27 +
) = 27 - 27 + 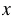 =
= 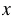 (км/ч).
(км/ч).
а) Чтобы найти расстояние, нужно время умножить на скорость движения.
Велосипедисты сближаются со скоростью 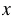 км/ч, тогда, учитывая то, что велосипедисты выехали одновременно из одного пункта, через 3 ч расстояние между ними станет равным: 3
км/ч, тогда, учитывая то, что велосипедисты выехали одновременно из одного пункта, через 3 ч расстояние между ними станет равным: 3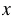 (км).
(км).
б) Чтобы найти значение буквенного выражения при заданном значении переменной, нужно в это выражение вместо буквы подставить числа, ей соответствующие, и выполнить вычисления (смотри решение).
в) Лишнее данное в условии - скорость первого велосипедиста, так как в ходе преобразований выражения для скорости удаления, скорость первого велосипедиста (27 км/ч) уходит и на дальнейшие результаты при решении задачи никак не влияет.
Вернуться к содержанию учебника