Задание 2.497 - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 1
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№2.497 учебника 2023-2024 (стр. 109):
Комбайнер на новом комбайне убрал зерно с поля за 56 ч и затратил времени на 30% меньше, чем на старом комбайне. Сколько времени потребовалось бы для выполнения этой работы на старом комбайне?
№2.497 учебника 2021-2022 (стр. 104):
У велосипеда, изобретенного крепостным уральским мастером Ефимом Артамоновым в 1800 г., переднее колесо было больше заднего. Длина окружности переднего колеса была равна 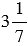 м, а заднего -
м, а заднего - 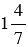 м. Сколько оборотов делало заднее колесо за
м. Сколько оборотов делало заднее колесо за 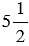 оборота переднего колеса?
оборота переднего колеса?
Подсказка
№2.497 учебника 2023-2024 (стр. 109):
Вспомните:
№2.497 учебника 2021-2022 (стр. 104):
Вспомните:
- Умножение обыкновенных дробей, взаимно обратные числа.
- Деление обыкновенных дробей.
- Смешанные числа.
- Неправильные дроби.
- Сокращение дробей.
- Деление и дроби.
Ответ
№2.497 учебника 2023-2024 (стр. 109):
Новый комбайн - 56 ч и на 30% меньше, чем старый.
Старый комбайн - ? ч
1) 100%-30%=70% - времени затратил новый комбайн.
70%=70:100=0,7.
2) 56:0,7=560:7=80 (ч) - затратил бы старый комбайн.
Ответ: старый комбайн затратил бы 80 ч.
Пояснения:
По условию новый комбайн затратил на уборку времени на 30% меньше, чем старый комбайн. Нам известно, что величина, от которой вычисляются проценты составляет 100 своих сотых долей, т.е. 100 %, тогда новый комбайн затратил 100%-30%=70% времени.
Переведем данное значение в десятичную дробь, для этого разделим число, стоящее перед знаком процентов на 100, получаем, что 70%=70:100=0,7. При этом нам дано, что он затратил 56 ч, то есть 56 ч соответствует 0,7 времени. Чтобы найти число по значению, соответствующему данной дроби, надо это значение разделить на дробь, тогда получаем, что старый комбайн затратил бы на уборку зерна 56:0,7=560:7=80 ч.
№2.497 учебника 2021-2022 (стр. 104):
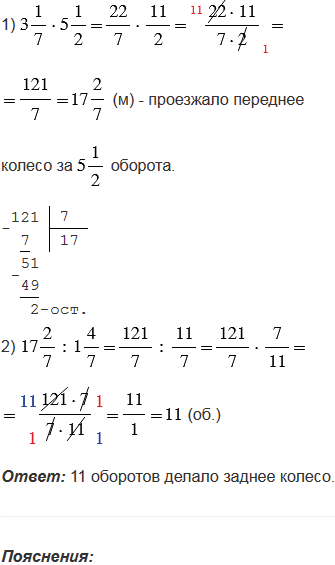

Правила, по которым выполнены вычисления:
1) чтобы выполнить умножение смешанных чисел, нужно записать эти числа в виде неправильных дробей, а затем воспользоваться правилом умножения дробей, произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель - произведению знаменателей;
2) чтобы выполнить деление смешанных чисел, нужно записать эти числа в виде неправильных дробей, а затем воспользоваться правилом деления дробей. Чтобы найти частное двух дробей, надо делимое умножить на число, обратное делителю. При этом помним, обратным числу является число .
Чтобы преобразовать смешанное число в неправильную дробь, надо целую часть числа умножить на знаменатель дробной части и к полученному произведению прибавить числитель дробной части; эту сумму записать как числитель неправильной дроби, а в ее знаменатель записать знаменатель дробной части смешанного числа.
При выполнении умножения дробей, чтобы вычисления были проще, не надо перемножать сразу, лучше сделать это после сокращения. Сократить дробь - значит, разделить ее числитель и знаменатель на одно и то же число (наибольший общий делитель).
Если при вычислениях получилась неправильная дробь (числитель больше знаменателя), ее нужно преобразовать в смешанное число. Чтобы неправильную дробь, числитель которой нацело не делится на знаменатель, преобразовать в смешанное число, надо числитель разделить на знаменатель; полученное неполное частное записать как целую часть смешанного числа, а остаток - как числитель его дробной части.
Дробь, у которой в знаменателе стоит единица, равна своему числителю.
Вернуться к содержанию учебника