Задание 2.71 - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 1
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№2.71 учебника 2023-2024 (стр. 52):
Определите с помощью линейки, какими числами(простыми или составными) являются натуральными числами 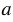 ,
, 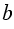 и
и 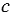 на рисунке 2.3. Запишите координаты точек K, N, D, М.
на рисунке 2.3. Запишите координаты точек K, N, D, М.

№2.71 учебника 2021-2022 (стр. 46):
Найдите все правильные дроби, знаменатель которых равен 16, а числитель и знаменатель - взаимно простые числа.
Подсказка
№2.71 учебника 2023-2024 (стр. 52):
Вспомните, какие числа называют простыми и составными.
№2.71 учебника 2021-2022 (стр. 46):
Вспомните:
- Обыкновенные дроби.
- Правильные и неправильные дроби.
- Наибольший общий делитель.
- Какие числа называют взаимно простыми.
Ответ
№2.71 учебника 2023-2024 (стр. 52):
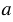 = 7 • 2 = 14 - составное число.
= 7 • 2 = 14 - составное число.
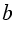 = 7 • 3 = 21 - составное число.
= 7 • 3 = 21 - составное число.
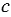 = 7 • 4 = 28 - составное число.
= 7 • 4 = 28 - составное число.
K(6 - 1) = K(5).
N(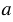 + 2) = N(14 + 2) = N(16).
+ 2) = N(14 + 2) = N(16).
D(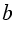 - 2) = D(21 - 2) = D(19).
- 2) = D(21 - 2) = D(19).
М(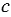 - 5) = М(28 - 5) = М(23).
- 5) = М(28 - 5) = М(23).
Пояснения:
Натуральное число называют простым, если оно имеет только два натуральных делителя: единицу и само это число.
Натуральное число называют составным, если оно имеет больше двух натуральных делителей.
№2.71 учебника 2021-2022 (стр. 46):
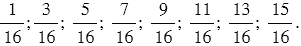
Пояснения:
Правильная дробь – это дробь, числитель которой меньше знаменателя, то есть правильными дробями со знаменателем 16 будут те, у которых числитель меньше 16. При этом числитель и знаменатель должны быть взаимно простыми числами, то есть их наибольший общий делитель должен быть равен 1.
НОД(1; 16) = 1;
НОД(2; 16) = 2;
НОД(3; 16) = 1;
НОД(4; 16) = 4;
НОД(5; 16) = 1;
НОД(6; 16) = 2;
НОД(7; 16) = 1;
НОД(8; 16) = 8;
НОД(9; 16) = 1;
НОД(10; 16) = 2;
НОД(11; 16) = 1;
НОД(12; 16) = 4;
НОД(13; 16) = 1;
НОД(14; 16) = 2;
НОД(15; 16) = 1.
То есть получаем, что правильные дроби, знаменатель которых равен 16, а числитель и знаменатель - взаимно простые числа - это:
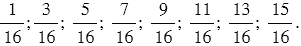
Вернуться к содержанию учебника