Задание 3.136 - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 1
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№3.136 учебника 2023-2024 (стр. 136):
Могут ли пересекаться:
а) два отрезка, симметричные относительно прямой;
б) два центрально-симметричных отрезка?
Ответы проиллюстрируйте рисунком.
№3.136 учебника 2021-2022 (стр. 146):
а) Начертите окружность Р и прямую 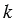 , не пересекающую эту окружность. Постройте окружность О, симметричную окружности Р относительно оси
, не пересекающую эту окружность. Постройте окружность О, симметричную окружности Р относительно оси 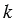 .
.
б) Постройте симметричную фигуру относительно точки С для четырехугольника на рисунке 84.
Подсказка
№3.136 учебника 2023-2024 (стр. 136):
Вспомните:
- Какие фигуры называют симметричными (осевая и центральная симметрии).
- Что называют отрезком.
№3.136 учебника 2021-2022 (стр. 146):
Вспомните, какие фигуры называют симметричными (центральная симметрия).
Ответ
№3.136 учебника 2023-2024 (стр. 136):
а) Два отрезка, симметричные относительно прямой, могут пересекаться.
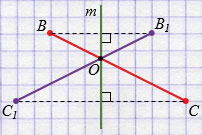
Отрезки ВС и В1С1 симметричны относительно прямой 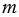 и они пересекаются в точке О.
и они пересекаются в точке О.
б) Два центрально-симметричных отрезка, не могут пересекаться, они могут иметь только одну общую точку.
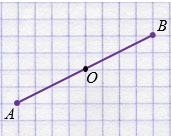
Отрезки АО и ОВ центрально-симметричны относительно точки О.
№3.136 учебника 2021-2022 (стр. 146):
а) Окружность О симметрична окружности Р относительно оси 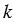 .
.
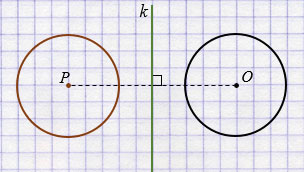
б) Четырехугольник А1В1СD1 симметричен четырехугольнику АВСD относительно точки С.
Пояснения:
а) Точки А и А1 называют симметричными относительно прямой 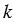 , если прямая
, если прямая 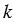 пересекает отрезок АА1 под прямым углом и делит его пополам.
пересекает отрезок АА1 под прямым углом и делит его пополам.
Чтобы построить окружность О, симметричную окружности Р относительно прямой 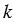 , сначала построим точку О, симметричную точке Р относительно прямой
, сначала построим точку О, симметричную точке Р относительно прямой 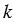 .
.
Проведем через точку Р прямую под прямым углом к прямой . Эта прямая пересечет ось симметрии в точке Е. Отложим на прямой РЕ отрезок ЕО, равный отрезку РЕ, по другую сторону от оси. Точка О симметрична точке Р относительно прямой 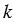 .
.
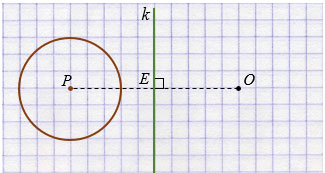
Далее с помощью циркуля строим окружность с центром О такого же радиуса как у окружности с центром Р.
Получаем окружность О, симметричную окружности Р относительно оси  .
.
б) Точки М и М1 называют симметричными относительно точки О, если точка О является серединой отрезка ММ1.
Чтобы построить четырехугольник, симметричный четырехугольнику АВСD относительно точки С, сначала построим точки симметричные вершинам четырехугольника АВСD относительно точки С.
На луче АС отложим отрезок СА1, равный отрезку АС. Точка А1 симметрична точке А относительно центра симметрии С. Аналогично строим точки В1 И D1, симметричные точкам В и D относительно центра симметрии С. Точка С симметрична сама себе. Точки А1 и В1, А1 и D1 соединим отрезками.

Четырехугольник А1В1СD1 симметричен четырехугольнику АВСD относительно точки С.
Вернуться к содержанию учебника