Осевая и центральная симметрии
Осевая симметрия
Точки А и А1 называют симметричными относительно прямой  , если прямая , если прямая  перпендикулярна отрезку АА1 и делит его пополам (смотри рисунок ниже). перпендикулярна отрезку АА1 и делит его пополам (смотри рисунок ниже). |
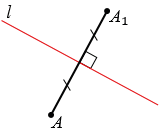
Рассмотрим построение точки, симметричной данной точке А относительно данной прямой  .
.
Пусть дана точка А и прямая  .
.
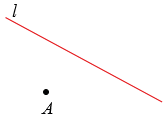
Точку симметричную точке А относительно прямой  , можно построить так. Проведем через точку А прямую
, можно построить так. Проведем через точку А прямую  , перпендикулярную прямой
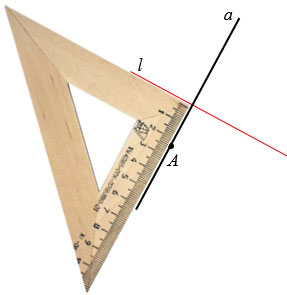
, перпендикулярную прямой  . Для этого используем чертежный угольник. Прикладываем чертежный угольник так, как показано на рисунке ниже и проводим прямую
. Для этого используем чертежный угольник. Прикладываем чертежный угольник так, как показано на рисунке ниже и проводим прямую  через точку А.
через точку А.
Пусть прямые  и
и  пересекаются в точке О. Отложим при помощи линейки на прямой
пересекаются в точке О. Отложим при помощи линейки на прямой  отрезок ОА1, равный отрезку ОА.
отрезок ОА1, равный отрезку ОА.
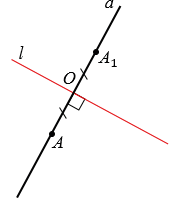
Получаем точки А и А1, которые симметричны относительно прямой  .
.
Также можно построить фигуры, симметричные относительно прямой.
Построим треугольник А1В1С1, симметричный треугольнику АВС относительно прямой  .
.
Пусть дан треугольник АВС и прямая  .
.
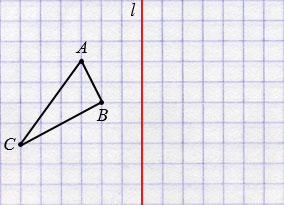
Далее строим точки А1, В1 и С1, симметричные точкам А, В и С относительно прямой  (алгоритм построения смотри выше), соединив которые получим треугольник А1В1С1, симметричный треугольнику АВС относительно прямой
(алгоритм построения смотри выше), соединив которые получим треугольник А1В1С1, симметричный треугольнику АВС относительно прямой  .
.
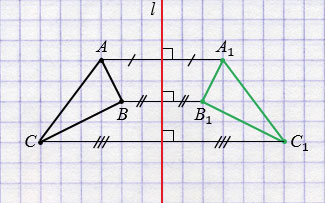
Обратите внимание, любые две фигуры, симметричные относительно прямой, равны.
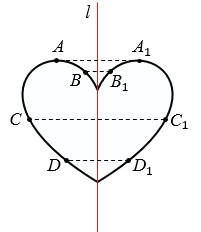
Если фигура имеет ось симметрии (прямая  ) то, все точки этой фигуры, не принадлежащие этой оси, можно разделить на пары симметричных точек.
) то, все точки этой фигуры, не принадлежащие этой оси, можно разделить на пары симметричных точек.
Центральная симметрия
| Точки М и М1 называют симметричными относительно точки О, если точка О является серединой отрезка ММ1 (смотри рисунок ниже). |
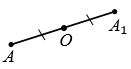
Рассмотрим построение точки, симметричной данной точке М относительно данной точки О.
Пусть даны точки М и О. Точку, симметричную точке М относительно точки О, можно построит так. Проведем луч МО.
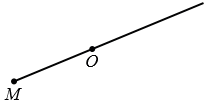
На луче МО отложим отрезок ОN , равный отрезку ОМ.
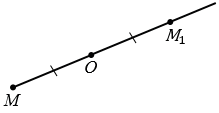
Точки М и М1, которые симметричны относительно точки О.
Также можно построить фигуры, симметричные относительно точки.
Построим треугольник А1В1С1, симметричный треугольнику АВС относительно точки О.
Пусть дан треугольник АВС и точки О.
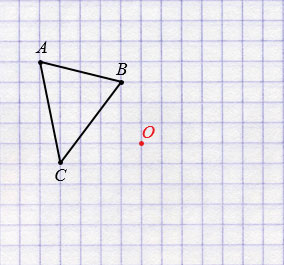
Далее строим точки А1, В1 и С1, симметричные точкам А, В и С относительно точки О (алгоритм построения смотри выше), соединив которые получим треугольник А1В1С1, симметричный треугольнику АВС относительно точки О.
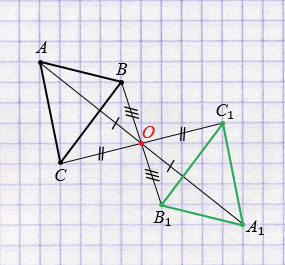
Обратите внимание, любые две фигуры, симметричные относительно точки, равны.
Рассмотрим окружность с центром в точке О. Все точки окружности можно разбить на пары точек, симметричных относительно точки О.
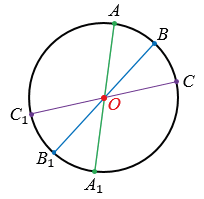
В таком случае говорят, что окружность имеет центр симметрии - точку О.
Также центр симметрии имеют такие фигуры, как отрезок, прямоугольник, эллипс.
Советуем посмотреть:
Правило встречается в следующих упражнениях:
5 класс
Задание 5.74, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
6 класс
Номер 1259, Мерзляк, Полонский, Якир, Учебник
Номер 1261, Мерзляк, Полонский, Якир, Учебник
Номер 1266, Мерзляк, Полонский, Якир, Учебник
Номер 1306, Мерзляк, Полонский, Якир, Учебник
Номер 1318, Мерзляк, Полонский, Якир, Учебник
Номер 10, Мерзляк, Полонский, Якир, Учебник
Задание 3.130, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 3.136, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 3.153, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание П.14, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
9 класс