Задание 3.115 - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 1. Страница 138
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№3.115 учебника 2023-2024 (стр. 138):
Объем призмы в 3 раза больше объема пирамиды, у которой высота и основание равны высоте и основанию призмы (рис. 3.8). Найдите объем четырехугольной пирамиды, в основании которой прямоугольник со сторонами  м и
м и 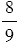 м, а высота равна 9 м.
м, а высота равна 9 м.
№3.115 учебника 2021-2022 (стр. 138):
Объем призмы в 3 раза больше объема пирамиды, у которой высота и основание равны высоте и основанию призмы (рис. 63). Найдите объем четырехугольной пирамиды, в основании которой прямоугольник со сторонами 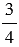 м и
м и 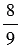 м, а высота равна 9 м.
м, а высота равна 9 м.
Подсказка
№3.115 учебника 2023-2024 (стр. 138):
№3.115 учебника 2021-2022 (стр. 138):
Вспомните:
- Что называют призмой, пирамидой.
- Как найти объем призмы.
- Умножение обыкновенных дробей.
- Сокращение дробей.
- Неправильные дроби.
Ответ
№3.115 учебника 2023-2024 (стр. 138):
№3.115 учебника 2021-2022 (стр. 138):
1) 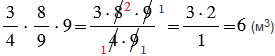 - объем призмы.
- объем призмы.
2) 6 : 3 = 2 (м3) - объем пирамиды.
Ответ: объем пирамиды равен 2 м3.
Пояснения:
Призма - это многогранник, у которого основания - равные многоугольники, параллельные друг другу, а боковые грани - параллелограммы. Призма, у которой в основании лежит прямоугольник является прямоугольным параллелепипедом. Объем прямоугольного параллелепипеда равен произведению трех его измерений (длины, ширины и высоты). Значит, объем данной призмы равен:
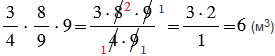 .
.
Произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель - произведению знаменателей. Чтобы умножить обыкновенную дробь на натуральное число, нужно ее числитель умножить на это число, а знаменатель оставить без изменения. При выполнении умножения дробей, чтобы вычисления были проще, не надо перемножать сразу, лучше сделать это после сокращения. Сократить дробь - значит, разделить ее числитель и знаменатель на одно и то же число (наибольший общий делитель).
Объем призмы в 3 раза больше объема пирамиды, у которой высота и основание равны высоте и основанию призмы, то есть объем такой пирамиды равен:
6 : 3 = 2 (м3).
Вернуться к содержанию учебника