Задание 2.556 - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 1. Страница 112

Пояснения:

В пунктах а) и б) в числителе и в знаменателе дробных выражений сначала преобразуем смешанные числа в неправильные дроби, а затем получаем из них натуральные числа, для этого в пункте а) числитель и знаменатель дробного выражения умножим на наименьший общий знаменатель чисел 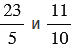, то есть на число 10, в пункте б) числитель и знаменатель дробного выражения умножим на наименьший общий знаменатель чисел 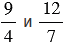, то есть на число 28. После выполнения умножения в пунктах а) и б) получатся неправильные дроби (числитель больше знаменателя), которые преобразуем в смешанные числа.

В пунктах в) и г), чтобы получить в числителе и в знаменателе дробного выражения натуральные числа, перенесем в них запятую вправо в каждом множителе на равное количество знаков, то есть так, чтобы общее количество знаков, на которые перенесена запятая в числителе и знаменателе дробного выражения было одинаковым, затем выполняем сокращение.

Чтобы преобразовать смешанное число в неправильную дробь, надо целую часть числа умножить на знаменатель дробной части и к полученному произведению прибавить числитель дробной части; эту сумму записать как числитель неправильной дроби, а в ее знаменатель записать знаменатель дробной части смешанного числа.

Чтобы умножить обыкновенную дробь на натуральное число, нужно ее числитель умножить на это число, а знаменатель оставить без изменения.

При выполнении умножения дробей, чтобы вычисления были проще, не надо перемножать сразу, лучше сделать это после сокращения. Сократить дробь - значит, разделить ее числитель и знаменатель на одно и то же число (наибольший общий делитель).

Чтобы неправильную дробь, числитель которой нацело не делится на знаменатель, преобразовать в смешанное число, надо числитель разделить на знаменатель; полученное неполное частное записать как целую часть смешанного числа, а остаток - как числитель его дробной части.

Также помним, дробь, у которой в знаменателе стоит единица, равна своему числителю.

Также, в пунктах а) и б) найти значения выражений, можно разделив числитель на знаменатель.

Чтобы найти частное двух дробей, надо делимое умножить на число, обратное делителю. При этом помним, обратным числу 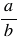является число .

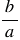Чтобы выполнить умножение смешанных чисел, нужно записать эти числа в виде неправильных дробей, а затем воспользоваться правилом умножения дробей.  Произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель - произведению знаменателей.