Задание 2.50 - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 1
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№2.50 учебника 2023-2024 (стр. 48):
Объем прямоугольного параллелепипеда равен 1001 см3. Найдите измерения параллелепипеда, если они выражаются натуральными числами и ни одно из них не равно 1 см.
№2.50 учебника 2021-2022 (стр. 43):
Какие из чисел 3552, 4712, 6576, 4836 делятся на 3 и на 4? Как вы думаете, числа, которые делятся на 3 и на 4, делятся на 12? Ответ обоснуйте.
Подсказка
№2.50 учебника 2023-2024 (стр. 48):
Вспомните:
- Что называют прямоугольным параллелепипедом, как найти его объем.
- Делители числа, разложение на множители.
- Умножение чисел.
№2.50 учебника 2021-2022 (стр. 43):
Ответ
№2.50 учебника 2023-2024 (стр. 48):
Делители числа 1001:
1, 7, 11, 13, 77, 91, 143, 1001.
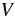 = 1001 см3 = 7 см • 11 см • 13 см
= 1001 см3 = 7 см • 11 см • 13 см
Ответ: измерения равны 7 см, 11 см и 13 см.
Пояснения:
Объем прямоугольного параллелепипеда равен произведению трех его измерений. Если 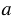 ,
, 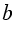 и
и 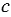 - измерения прямоугольного параллелепипеда, то его объем:
- измерения прямоугольного параллелепипеда, то его объем: 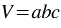 .
.
По условию объем прямоугольного параллелепипеда равен 1001 см3, получается, чтобы найти измерения такого параллелепипеда, нужно разложить число 1001 на три множителя, каждый множитель будет соответствовать какому-то одному измерению параллелепипеда.
Чтобы разложить число 1001 на множители, найдем делители числа 1001: 1, 7, 11, 13, 77, 91, 143, 1001.
Значит, измерения параллелепипеда равны 7 см, 11 см, 13 см, так как только произведение этих трех чисел даст нам нужное число 1001.
№2.50 учебника 2021-2022 (стр. 43):
3552 - делится на 4, так как 52 делится на 4, и делится на 3, так как
3 + 5 + 5 + 2 = 15 - делится на 3.
4712 - делится на 4, так как 12 делится на 4, и не делится на 3, так как
4 + 7 + 1 + 2 = 14 - не делится на 3.
6576 - делится на 4, так как 76 делится на 4, и делится на 3, так как
6 + 5 + 7 + 6 = 24 - делится на 3.
4836 - делится на 4, так как 36 делится на 4, и делится на 3, так как
4 + 8 + 3 + 6 = 21 - делится на 3.
Ответ: на 3 и 4 делятся числа 3552, 6576 и 48 36.
Числа, которые делятся на 3 и на 4, делятся на 12, так как 3 • 4 = 12.
Пояснения:
Чтобы определить числа, которые делятся на 3 и на 4, не нужно выполнять деление на 3 и на 4, можно просто вспомнить признаки делимости на 3 и на 4.
Признак делимости на 4:
если две последние цифры числа образуют число, которое делится на 4, то и само число делится на 4.
Признак делимости на 3:
если сумма цифр числа делится на 3, то и число делится на 3.
Вернуться к содержанию учебника