Задание 2.21 - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 1

Пусть 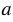= 20 см, 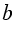и 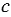- измерения прямоугольного параллелепипеда, тогда его объем:

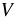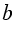
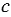= 20 (см³)

а) Объем данного прямоугольного параллелепипеда всегда будет выражаться числом, кратным 2, так как 20 делится нацело на 2.

б) Объем данного прямоугольного параллелепипеда не всегда будет выражаться числом, кратным 3, так как 20 не делится нацело на 3 (объем будет выражаться числом кратным 3 только тогда, когда 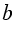или 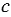кратно 3).

в) Объем данного прямоугольного параллелепипеда всегда будет выражаться числом, кратным 4, так как 20 делится нацело на 4.

г) Объем данного прямоугольного параллелепипеда всегда будет выражаться числом, кратным 5, так как 20 делится нацело на 5.

д) Объем данного прямоугольного параллелепипеда не всегда будет выражаться числом, кратным 6, так как 20 не делится нацело на 6 (объем будет выражаться числом кратным 6 только тогда, когда 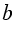или 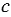кратно 3, так как 20 кратно 2, а 2 • 3 = 6).

Пояснения:

Объем прямоугольного параллелепипеда равен произведению трех его измерений.

Помним, если в произведении хотя бы один из множителей делится на какое-то число, то и все произведение  делится на это число.

а) Контрпример:

число 65 оканчивается цифрой 5, но оно не делится на 7.

б) Контрпример:

число 21 не оканчивается цифрой 7, но оно делится на 7.

Пояснения:

Пример, опровергающий верность некоторого утверждения, называют контрпримером.