Страница 76. Урок 25 - ГДЗ Математика 4 класс. Петерсон. Учебник часть 1
Вернуться к содержанию учебника
Страница 73. Урок 24 Страница 74. Урок 24 Страница 75. Урок 25 Страница 76. Урок 25 Страница 77. Урок 26 Страница 78. Урок 26 Страница 79. Урок 27
Вопрос
Задание № 5. Мотоциклист за день проехал некоторое расстояние. 1 % пути он ехал по просёлочной дороге, что составило 3 км. Остальную часть пути он ехал по шоссе. Сколько километров ехал мотоциклист по шоссе?
Ответ
Решение
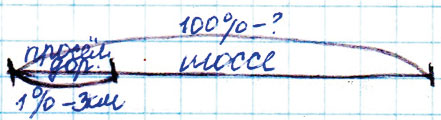
1) 100 - 1 = 99 % по шоссе.
2) 3 • 99 = 297 (км)
| × | 9 | 9 |
| 3 | ||
| 2 | 9 | 7 |
Ответ: 297 км ехал мотоциклист по шоссе.
Пояснение
Процент - одна сотая часть числа.
Вопрос
Задание № 6. Единица разделена на 24 равные части. Сколько таких частей содержит 1/24, 1/12, 1/8, 1/6, 1/4, 1/3, 1/2 доля? Отметь эти числа на числовом луче.
Ответ
Вопрос
Задание № 8. Прочитай неравенство и найди множество его натуральных решений.
Подсказка
Повтори, что такое неравенства.
Ответ
Решение
а) {5, 6, 7, 8}
б) {7, 8, 9, 10, 11}
Пояснение
Двойные неравенства – неравенства, в записи которых используется два знака сравнения.
Вопрос
Задание № 9. Составь программу действий и вычисли:
| а) (492345 - 264174) : 57 + 26 • 693 - 88592 : 98; |
| б) 307 • (30405 - 29596) + 765000 : (317 + 533) - 226896 : 87. |
Подсказка
Ответ
Вопрос
Задание № 10. На одной планете живут 40 колиордов. 12 из них вечером пьют чай, 28 - смотрят телевизор, а 5 не делают ни того ни другого, так как рано ложатся спать. Сколько колиордов пьют по вечерам чай, смотря телевизор?
Подсказка
Повтори, что такое окружность.
Ответ
Решение
1) 40 - 5 = 35 (к.) - смотрят телевизор или пьют чай.
2) (28 + 12) - 35 = 5 (к.)
Ответ: 5 колиордов пьют чай, смотря телевизор.
Пояснение
Пересечение множеств А и В - это их общая часть.
Чтобы найти пересечение множеств А и В, нужно взять все элементы, принадлежащие одновременно как множеству А, так и множеству В.
Вернуться к содержанию учебника