Задание 285 - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№285 учебника 2013-2022 (стр. 86):
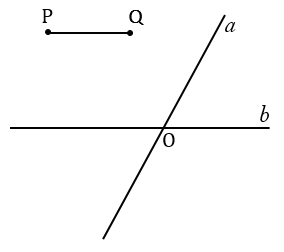
Даны пересекающиеся прямые 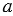 и
и 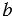 и отрезок РQ. На прямой
и отрезок РQ. На прямой 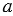 постройте точку, удаленную от прямой
постройте точку, удаленную от прямой 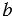 на расстояние РQ.
на расстояние РQ.
№285 учебника 2023-2024 (стр. 85):
Расстояние между параллельными прямыми 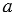 и
и 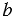 равно 3 см, а между параллельными прямыми
равно 3 см, а между параллельными прямыми 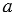 и
и 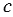 равно 5 см. Найдите расстояние между прямыми
равно 5 см. Найдите расстояние между прямыми 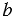 и
и 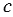 .
.
Подсказка
№285 учебника 2013-2022 (стр. 86):
Вспомните:
- Какие прямые называются пересекающимися.
- Что такое отрезок.
- Что такое расстояние от точки до прямой.
- Как построить перпендикулярные прямые.
- Какие прямые называются перпендикулярными.
№285 учебника 2023-2024 (стр. 85):
Вспомните:
- Какие прямые называются параллельными.
- Что такое расстояние между параллельными прямыми.
- Следствия из аксиомы параллельных прямых.
Ответ
№285 учебника 2013-2022 (стр. 86):
Дано: 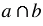 = О, PQ - отрезок.
= О, PQ - отрезок.
Построить: точку на прямой 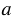 постройте точку, удаленную от прямой
постройте точку, удаленную от прямой 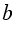 на расстояние РQ
на расстояние РQ
Решение:
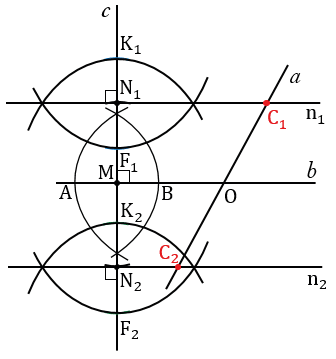
Ответ: два решения - точки С1 и С2.
Пояснения:
С помощью линейки проводим отрезок PQ и пересекающиеся прямые 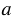 и
и 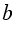 , точку пересечения этих прямых обозначаем О.
, точку пересечения этих прямых обозначаем О.
На прямой 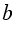 отмечаем точку М и проводим через нее прямую
отмечаем точку М и проводим через нее прямую 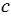 , перпендикулярную прямой
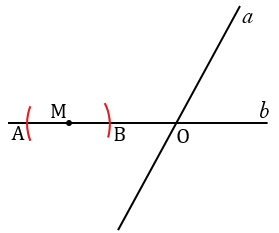
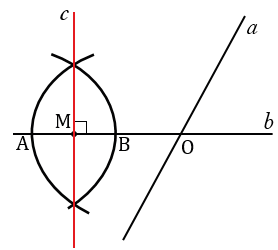
, перпендикулярную прямой 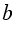 . С помощью циркуля откладываем равные отрезки МА и МВ (МА = МВ). Для этого строим окружность с центром в точке М, при этом всю окружность строить не обязательно, достаточно сделать пометки по разные стороны от точки М (смотри выделенное красным).
. С помощью циркуля откладываем равные отрезки МА и МВ (МА = МВ). Для этого строим окружность с центром в точке М, при этом всю окружность строить не обязательно, достаточно сделать пометки по разные стороны от точки М (смотри выделенное красным).
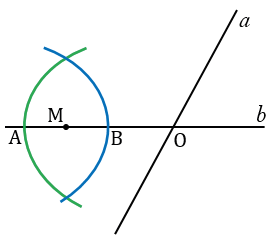
Затем строим две окружности с центрами в точках А и В радиуса АВ (полностью окружности строить не обязательно, смотри выделенное синим и зеленым цветом).
Данные окружности пересекаются в двух точках, через которые проводим прямую 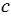 , перпендикулярную к прямой
, перпендикулярную к прямой 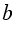 .
.
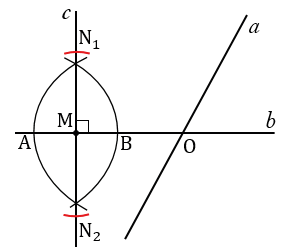
Далее, откладываем от точки М на прямой отрезки МN1 = РQ и МN2 = РQ. Для этого строим окружность с центром в точке М радиуса PQ, при этом всю окружность строить не обязательно, достаточно сделать пометки по разные стороны от точки М прямой (смотри выделенное красным).
Затем, через точки N1 и N2 строим прямые n1 и n2, перпендикулярные к прямой 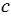 . С помощью циркуля откладываем равные отрезки N1К1 и N1F1 (N1К1 = N1F1). Для этого строим окружность с центром в точке N1, при этом всю окружность строить не обязательно, достаточно сделать пометки по разные стороны от точки N1 (смотри выделенное синим цветом). И также с помощью циркуля откладываем равные отрезки N2К2 и N2F2 (N2К2 = N2F2). Для этого строим окружность с центром в точке N2, при этом всю окружность строить не обязательно, достаточно сделать пометки по разные стороны от точки N2 (смотри выделенное зеленым цветом).
. С помощью циркуля откладываем равные отрезки N1К1 и N1F1 (N1К1 = N1F1). Для этого строим окружность с центром в точке N1, при этом всю окружность строить не обязательно, достаточно сделать пометки по разные стороны от точки N1 (смотри выделенное синим цветом). И также с помощью циркуля откладываем равные отрезки N2К2 и N2F2 (N2К2 = N2F2). Для этого строим окружность с центром в точке N2, при этом всю окружность строить не обязательно, достаточно сделать пометки по разные стороны от точки N2 (смотри выделенное зеленым цветом).
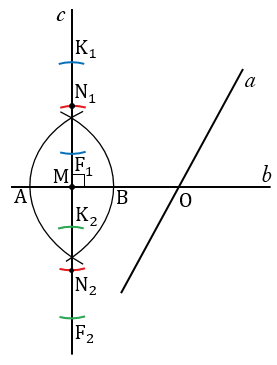
Затем строим две окружности с центрами в точках К1 и F1 радиуса К1F1, и две окружности с центрами в точках К2 и F2 радиуса К2F2 (полностью окружности строить не обязательно, смотри выделенное фиолетовым и оранжевым цветом).
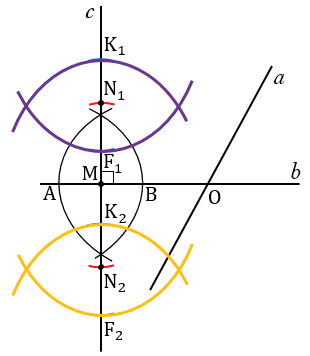
Каждая пара окружностей пересекаются в двух точках, через эти точки проводим прямые n1 и n2.
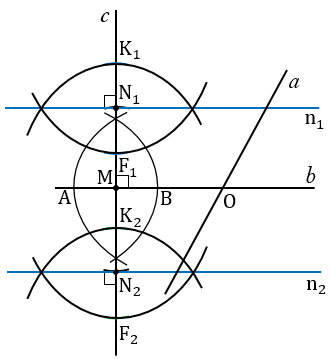
Точки пресечения прямых n1 и n2 с прямой  обозначим С1 и С2 соответственно.
обозначим С1 и С2 соответственно.
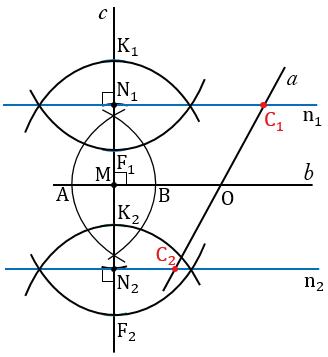
Точки С1 и С2 удалены от прямой 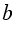 на расстояние равное длине отрезка РQ и лежат на прямой
на расстояние равное длине отрезка РQ и лежат на прямой 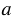 , т.е. точки С1 и С2 - искомые точки, значит, данная задача имеет два решения (точки расположенные по разные стороны от прямой
, т.е. точки С1 и С2 - искомые точки, значит, данная задача имеет два решения (точки расположенные по разные стороны от прямой 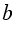 ).
).
№285 учебника 2023-2024 (стр. 85):
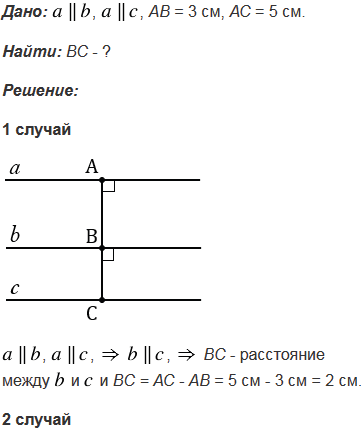



Вернуться к содержанию учебника