Номер 471 - ГДЗ Алгебра 8 класс. Мерзляк, Полонский. Учебник. Страница 121
Вернуться к содержанию учебника
Упражнения §15. Страница 121
Вопрос
Истинным или ложным является высказывание:
1) любое натуральное число является целым;
2) любое натуральное число является рациональным;
3) любое натуральное число является действительным;
4) любое рациональное число является целым;
5) любое действительное число является рациональным;
6) любое рациональное число является действительным;
7) любое иррациональное число является действительным;
8) любое действительное число является рациональным или иррациональным?
Подсказка
Вспомните:
- Что называют множеством.
- Что называют элементом множества.
- Что называют подмножеством данного множества.
- Что такое объединение множеств.
- Числовые множества.
Ответ
1) любое натуральное число является целым - истинно;
2) любое натуральное число является рациональным - истинно;
3) любое натуральное число является действительным - истинно;
4) любое рациональное число является целым - ложно;
5) любое действительное число является рациональным - ложно;
6) любое рациональное число является действительным - истинно;
7) любое иррациональное число является действительным - - истинно;
8) любое действительное число является рациональным или иррациональным - истинно.
Пояснения:
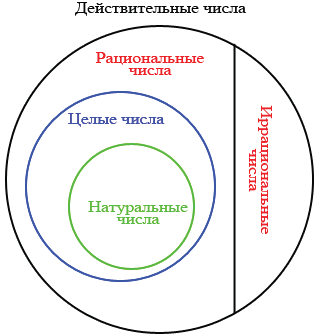
Словом "множество" в математическом языке обозначают любую совокупность объектов или предметов, объединенных каким-либо общим признаком. Все натуральные числа образуют множество натуральных чисел. Данное множество обозначается буквой N. Все натуральные числа, противоположные им числа и число нуль образуют множество целых чисел. Данное множество обозначают буквой Z. Целые и дробные (как положительные, так и отрицательные) числа образуют множество рациональных чисел. Данное множество обозначают буквой Q. Объединение множеств иррациональных и рациональных чисел называют множеством действительных чисел, данное множество обозначают буквой R.
То есть мы можем записать, что:
N 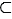 Z
Z 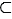 Q
Q 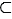 R.
R.
Иллюстрацией связи между числовыми множествами, которые рассмотрены выше, может служить схема:
Вернуться к содержанию учебника