Упражнение 292 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№292 учебника 2023-2025 (стр. 67):
Измеряя через каждую минуту температуру воды в баке в процессе нагревания, составили таблицу:
Постройте график зависимости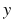 
(
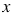) (масштаб: 1 см на оси 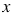соответствует 1 мин, 1 см на оси 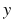соответствует 10 0С). Используя график, ответьте на вопросы:
а) Какую температуру имела вода через 4 мин; через 5,5 мин, через 9 мин, через 9,7 мин после начала нагревания?
б) Через сколько минут после начала нагревания температура воды стала равной 41 0С; 60 0С; 99 0С?
в) В какой промежуток времени процесс нагревания происходил интенсивнее всего?
г) Через сколько минут после начала нагревания вода закипела?
д) Сколько секунд кипела вода?
е) В какое время температура воды стала равна 98 0С?
№292 учебника 2013-2022 (стр. 68):
Измеряя через каждую минуту температуру воды в баке в процессе нагревания, составили таблицу:
Постройте график зависимости \(y\) от \(x\) (масштаб: 1 см на оси \(x\) соответствует 1 мин, 1 см на оси \(y\) соответствует 10 0С). Используя график, ответьте на вопросы:
а) Какую температуру имела вода через 4 мин; через 5,5 мин, через 9 мин, через 10,7 мин после начала нагревания?
б) Через сколько минут после начала нагревания температура воды стала равной 41 0С; 60 0С; 95 0С?
Подсказка
№292 учебника 2023-2025 (стр. 67):
№292 учебника 2013-2022 (стр. 68):
Ответ
№292 учебника 2023-2025 (стр. 67):
№292 учебника 2013-2022 (стр. 68):
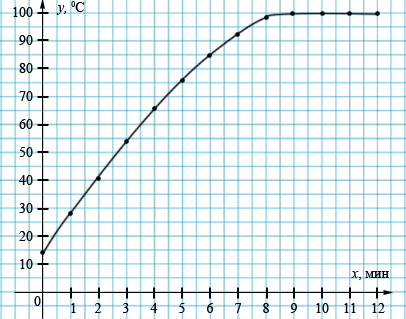
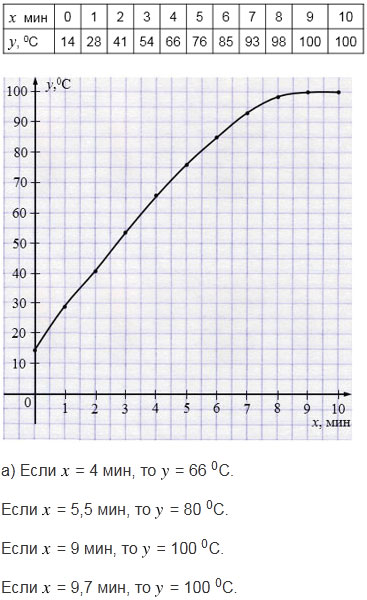
а) Если \(x\)= 4 мин, то \(y\) = 66 0С.
Если \(x\) = 5,5 мин, то \(y\) = 81 0С.
Если \(x\) = 9 мин, то \(y\) = 100 0С.
Если \(x\) = 10,7 мин, то \(y\) = 100 0С.
б) Если \(y\) = 41 0С, то \(x\) = 2 мин.
Если \(y\) = 60 0С, то \(x\) = 3,5 мин.
Если \(y\) = 95 0С, то \(x\) = 7,5 мин.
Пояснения:
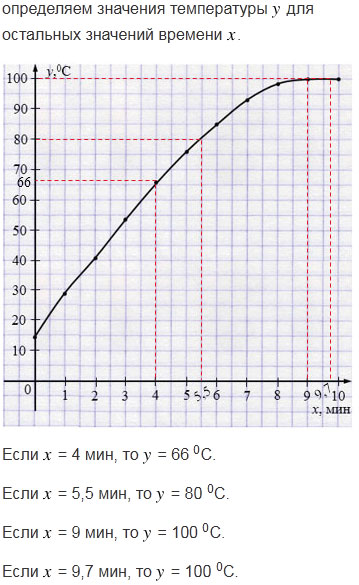
а) Чтобы определить значение температуры \(y\) через время \(x\) , равное 4 мин, нужно через точку оси \(x\) с абсциссой, равной 4, провести перпендикуляр к оси \(x\) . Точка пересечения этого перпендикуляра с графиком функции имеет координаты (4; 66). Значит, через \(x\) = 4 мин значение температуры \(y\) = 66 0С. Аналогично определяем значения температуры \(y\) для остальных значений времени \(x\).
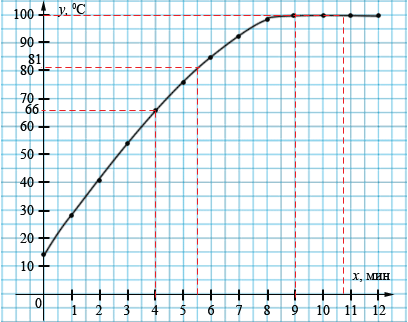
Если \(x\)= 4 мин, то \(y\) = 66 0С.
Если \(x\) = 5,5 мин, то \(y\) = 81 0С.
Если \(x\) = 9 мин, то \(y\) = 100 0С.
Если \(x\) = 10,7 мин, то \(y\) = 100 0С.
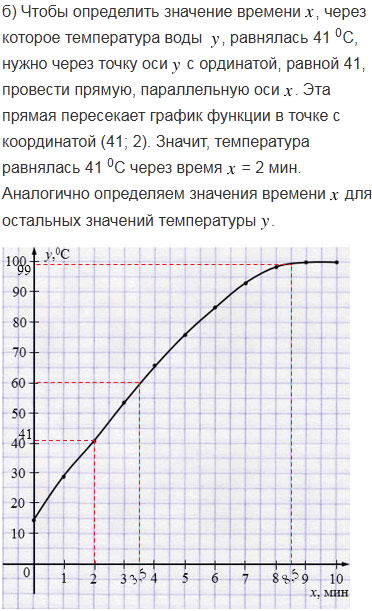
б) Чтобы определить значение времени \(x\), через которое температура воды \(y\), равнялась 41 0С, нужно через точку оси \(y\) с ординатой, равной 41, провести прямую, параллельную оси \(x\). Эта прямая пересекает график функции в точке с координатой (41; 2). Значит, температура равнялась 41 0С через время \(x\) = 2 мин. Аналогично определяем значения времени \(x\) для остальных значений температуры \(y\).
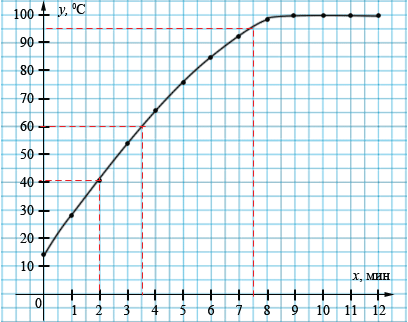
Если \(y\) = 41 0С, то \(x\) = 2 мин.
Если \(y\) = 60 0С, то \(x\) = 3,5 мин.
Если \(y\) = 95 0С, то \(x\) = 7,5 мин.
Вернуться к содержанию учебника