Задание 6.91 - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 2. Страница 114
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
№6.91 учебника 2021-2022 (стр. 114):
Графики движения грузового автомобиля (график АВ) и мотоцикла (график МN) из одного города изображены на рисунке 84. Определите по данным графикам:
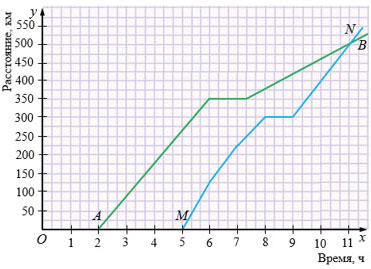
Рис. 84
а) время выезда грузового автомобиля и мотоцикла из города;
б) расстояние от города до мотоцикла в 6 ч 40 мин; в 9 ч;
в) расстояние от города до грузового автомобиля в 5 ч 20 мин; в 9 ч;
г) время, когда грузовой автомобиль находился в 325 км от города; в 425 км от города;
д) время, когда мотоцикл находился в 325 км от города; в 425 км от города;
е) останавливались ли грузовой автомобиль и мотоцикл; сколько времени длились остановки;
ж) на каком расстоянии от города и в какое время мотоцикл догнал грузовой автомобиль;
з) в какое время грузовой автомобиль двигался с постоянной скоростью;
и) скорость грузового автомобиля между 3 ч и 4 ч; между 8 ч и 9 ч;
к) расстояние между грузовым автомобилем и мотоциклом в 6 ч; в 10 ч;
л) среднюю скорость грузового автомобиля и среднюю скорость мотоцикла до времени их встречи.
Подсказка
№6.91 учебника 2021-2022 (стр. 114):
Вспомните:
- Положение точек на координатной плоскости.
- Представление числовой информации в графиках.
- Перпендикулярные прямые.
- Деление и дроби.
- Смешанные числа.
- Неправильные дроби.
- Деление с остатком.
- Задачи на движение.
Ответ
№6.91 учебника 2021-2022 (стр. 114):
а) Время выезда из города:
грузового автомобиля - 2 ч;
мотоцикла - 5 ч.
б) Расстояние от города до мотоцикла:
в 6 ч 40 мин - 190 км;
в 9 ч - 300 км.
в) Расстояние от города до грузового автомобиля:
в 5 ч 20 мин - 290 км;
в 9 ч - 420 км.
г) Время, когда грузовой автомобиль находился:
в 325 км от города - 5 ч 40 мин;
в 425 км от города - в 9 ч 10 мин.
д) Время, когда мотоцикл находился:
в 325 км от города - 9 ч 20 мин;
в 425 км от города - 10 ч 20 мин.
е) Грузовой автомобиль и мотоцикл останавливались.
Остановка грузового автомобиля длилась с 6 ч до 7 ч 20 мин, то есть
1 ч 20 мин.
Остановка мотоцикла длилась с 8 ч до 9 ч, то есть 1 ч.
ж) В 11 ч на расстоянии 500 км от города ч мотоцикл догнал грузовой автомобиль.
з) Грузовой автомобиль двигался с постоянной скоростью
с 2 ч до 6 и с 7 ч 20 мин до 11 ч 20 мин.
и) 1) В 3 ч - 87 км от города,
в 4 ч - 175 км от города,
с 3 ч до 4 ч грузовой автомобиль проехал:
175 - 87 = 88 (км), тогда его скорость с 3 ч до 4 ч равна 88 км/ч.
2) В 8 ч - 375 км от города,
в 9 ч - 420 км от города,
с 8 ч до 9 ч грузовой автомобиль проехал:
420 - 375 = 45 (км), тогда его скорость с 8 ч до 9 ч равна 45 км/ч.
к) 1) Грузовой в 6 ч - 350 км от города,
мотоцикл в 6 ч - 125 км от города,
расстояние между ними в 6 ч:
350 - 125 = 225 (км).
2) Грузовой в 10 ч - 460 км от города,
мотоцикл в 10 ч - 400 км от города,
расстояние между ними в 10 ч:
460 - 400 = 60 (км).
л) Время встречи - 11 ч,
Расстояние от города - 500 км.
1) 11 - 2 = 9 (ч) - общее время в пути грузового автомобиля.
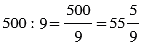 (км/ч) - средняя скорость грузового автомобиля.
(км/ч) - средняя скорость грузового автомобиля.
| - | 5 | 0 | 0 | 9 | ||||
| 4 | 5 | 5 | 5 | |||||
| - | 5 | 0 | ||||||
| 4 | 5 | |||||||
| 5 | - | о | с | т | . |
2) 11 - 5 = 6 (ч) - общее время в пути мотоцикла.
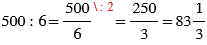 (км/ч) - средняя скорость мотоцикла.
(км/ч) - средняя скорость мотоцикла.
| - | 2 | 5 | 0 | 3 | |||||||||||
| 2 | 4 | 8 | 3 | ||||||||||||
| - | 1 | 0 | |||||||||||||
| 9 | |||||||||||||||
| 1 | - | о | с | т | . |
Пояснения:
а) Когда грузовой автомобиль и мотоцикл вышли из города расстояние до них было равно 0 км, то есть нам надо найти точки пересечения графиков с осью абсцисс (осью  ). То есть грузовой автомобиль вышел из города в 2 ч, а мотоцикл - в 5 ч.
). То есть грузовой автомобиль вышел из города в 2 ч, а мотоцикл - в 5 ч.
б) Определим на каком расстоянии от города был мотоцикл в 6 ч 40 мин. Для этого найдем на оси абсцисс (ось 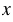 ) деление, соответствующее времени 6 ч 40 мин, затем в данной точке проведем перпендикуляр к оси
) деление, соответствующее времени 6 ч 40 мин, затем в данной точке проведем перпендикуляр к оси 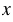 до пересечения с графиком МN. Далее проводим из полученной точки перпендикуляр к оси ординат (ось
до пересечения с графиком МN. Далее проводим из полученной точки перпендикуляр к оси ординат (ось 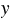 ). Тогда точка, в которую придет перпендикуляр на оси
). Тогда точка, в которую придет перпендикуляр на оси 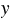 , укажет на расстояние до города в данный момент времени. То есть мы получаем, мотоцикл в 6 ч 40 мин был от города на расстоянии 190 км. Аналогично находим, что в 9 ч мотоцикл был на расстоянии 300 км от города.
, укажет на расстояние до города в данный момент времени. То есть мы получаем, мотоцикл в 6 ч 40 мин был от города на расстоянии 190 км. Аналогично находим, что в 9 ч мотоцикл был на расстоянии 300 км от города.

в) Определим на каком расстоянии от города был грузовой автомобиль в 5 ч 20 мин. Для этого найдем на оси абсцисс (ось 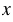 ) деление, соответствующее времени 5 ч 420 мин, затем в данной точке проведем перпендикуляр к оси
) деление, соответствующее времени 5 ч 420 мин, затем в данной точке проведем перпендикуляр к оси 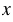 до пересечения с графиком АВ. Далее проводим из полученной точки перпендикуляр к оси ординат (ось
до пересечения с графиком АВ. Далее проводим из полученной точки перпендикуляр к оси ординат (ось 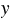 ). Тогда точка, в которую придет перпендикуляр на оси
). Тогда точка, в которую придет перпендикуляр на оси 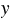 , укажет на расстояние до города в данный момент времени. То есть мы получаем, грузовой автомобиль в 5 ч 20 мин был от города на расстоянии 290 км. Аналогично находим, что в 9 ч грузовой автомобиль был на расстоянии 420 км от города.
, укажет на расстояние до города в данный момент времени. То есть мы получаем, грузовой автомобиль в 5 ч 20 мин был от города на расстоянии 290 км. Аналогично находим, что в 9 ч грузовой автомобиль был на расстоянии 420 км от города.
г) Определим в какое время грузовой автомобиль находился в 325 км от города. Для этого найдем на оси ординат (ось 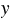 ) деление, соответствующее расстоянию до города в 325 км, затем в данной точке проведем перпендикуляр к оси
) деление, соответствующее расстоянию до города в 325 км, затем в данной точке проведем перпендикуляр к оси 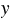 до пересечения с графиком АВ. Далее проводим из полученной точки перпендикуляр к оси абсцисс (ось
до пересечения с графиком АВ. Далее проводим из полученной точки перпендикуляр к оси абсцисс (ось 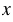 ). Тогда, в которую придет перпендикуляр на оси
). Тогда, в которую придет перпендикуляр на оси 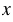 , укажет момент времени, в который грузовой автомобиль был на расстоянии 325 км от города. То есть мы получаем, что грузовой автомобиль находился в 325 км от города в 5 ч 40 мин. Аналогично находим, грузовой автомобиль находился на расстоянии 425 км от города в 9 ч 10 мин.
, укажет момент времени, в который грузовой автомобиль был на расстоянии 325 км от города. То есть мы получаем, что грузовой автомобиль находился в 325 км от города в 5 ч 40 мин. Аналогично находим, грузовой автомобиль находился на расстоянии 425 км от города в 9 ч 10 мин.
д) Аналогично пункту г) определяем, что мотоциклист находился в 325 км от города в 9 ч 20 мин, а в 425 км от города - в 10 ч 20 мин.

е) Остановки на графике определяют горизонтальные участки. Горизонтальные участки есть на каждом графике, значит, и грузовой автомобиль и мотоцикл останавливались.
Остановка грузового автомобиля длилась с 6 ч до 7 ч 20 мин, то есть
1 ч 20 мин.
Остановка мотоцикла длилась
с 8 ч до 9 ч, то есть 1 ч.

ж) Чтобы определить, в какое время и на каком расстоянии от города мотоцикл догнал грузовой автомобиль. Нам необходимо найти точку пересечения графиков, а затем из нее опустить перпендикуляры к осям. Тогда на оси абсцисс мы найдем момент времени, а на оси ординат расстояние до города. Получаем, что в 11 ч на расстоянии 500 км от города мотоциклист догнал грузовой автомобиль.

з) Грузовой автомобиль двигался с постоянной скоростью
с 2 ч до 6 и с 7 ч 20 мин до 11 ч 20 мин.
и) Чтобы определить скорость грузового автомобиля между 3 ч и 4 ч, надо сначала определить расстояние, на котором находился грузовой автомобиль в каждый момент времени (см пункт в).
В 3 ч грузовой автомобиль находился на расстоянии 87 км от города, в 4 ч - на расстоянии 175 км от города, значит, за час с 3 ч до 4 ч грузовой автомобиль проехал 175 - 87 = 88 (км), то есть его скорость с 3 ч до 4 ч равна 88 км/ч.

В 8 ч грузовой автомобиль находился на расстоянии 375 км от города, в 9 ч - на расстоянии 420 км от города, значит, за час с 8 ч до 9 ч грузовой автомобиль проехал 420 - 375 = 45 (км), то есть его скорость с 8 ч до 9 ч равна 45 км/ч.

к) Определим на каком расстоянии друг от друга были грузовой автомобиль и мотоцикл в 6 ч. Для этого сначала определим на каком расстоянии от города находился грузовой автомобиль и мотоцикл в 6 ч (см. пункт б), а затем из большего расстояния вычитаем меньшее.
Грузовой автомобиль в 6 ч был на расстоянии 350 км от города, а мотоцикл - на расстоянии 125 км от города, то есть расстояние между ними в 6 ч было равно 350 - 125 = 225 (км).

Грузовой автомобиль в 10 ч был на расстоянии 460 км от города, а мотоцикл - на расстоянии 400 км от города, то есть расстояние между ними в 10 ч было равно 460 - 400 = 60 (км).

л) Чтобы найти среднюю скорость, надо все пройденное расстояние разделить на общее время в пути.
Грузовой автомобиль и мотоцикл встретились в 11 ч.
Грузовой автомобиль выехал из города в 2 ч, значит, до встречи с мотоциклом грузовой автомобиль был в пути
11 - 2 = 9 (ч).
Встреча произошла на расстоянии 500 км от города, значит, средняя скорость грузового автомобиля:
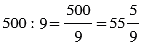 (км/ч).
(км/ч).
Мотоцикл выехал из города в 5 ч, значит, до встречи с грузовым автомобилем мотоцикл был в пути
11 - 5 = 6(ч).
Встреча произошла на расстоянии 500 км от города, значит, средняя скорость мотоцикла:
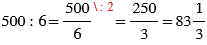 (км/ч).
(км/ч).
Вернуться к содержанию учебника