Задание 6.228 - ГДЗ Математика 5 класс. Виленкин, Жохов. Учебник часть 2
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№6.228 учебника 2023-2024 (стр. 126):
Обратите обыкновенную дробь в десятичную и найдите значение выражения:
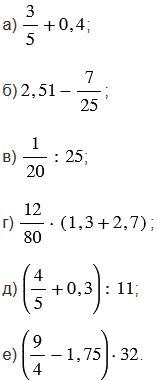
№6.228 учебника 2021-2022 (стр. 110):
Найдите корень уравнения:
а) (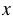 - 7,38) • 4 = 18;
- 7,38) • 4 = 18;
б) (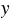 + 0,7) : 3 = 2,69.
+ 0,7) : 3 = 2,69.
Подсказка
№6.228 учебника 2023-2024 (стр. 126):
Вспомните:
- Обыкновенные дроби.
- Десятичную запись дробных чисел.
- Деление десятичных дробей на натуральное число.
- Умножение десятичных дробей на натуральное число
- Сложение и вычитание десятичных дробей.
- Порядок выполнения действий.
№6.228 учебника 2021-2022 (стр. 110):
Вспомните:
- Что называется уравнением, его корни.
- Десятичные дроби.
- Сложение и вычитание десятичных дробей.
- Умножение и деление десятичных дробей на натуральное число.
Ответ
№6.228 учебника 2023-2024 (стр. 126):
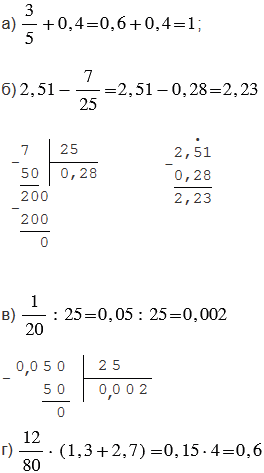
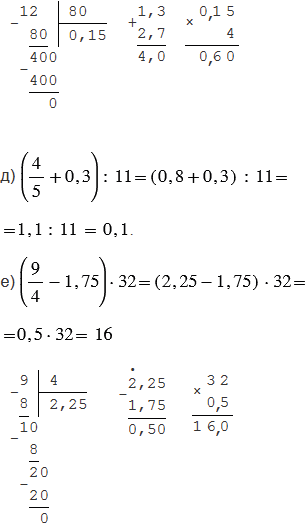
Пояснения:
С помощью деления находят десятичную дробь, равную данной обыкновенной дроби.
Другими словами, с помощью деления обращают обыкновенную дробь в десятичную. Для этого необходимо числитель дроби разделить на ее знаменатель.
Разделить десятичную дробь на натуральное число - значит найти такую дробь, которая при умножении на это натуральное число даёт делимое.
Правила вычислений с десятичными дробями смотри в подсказке.
Если целая часть меньше делителя, то частное начинается с нуля целых.
При этом помним, любое натуральное число можно представить в виде десятичной дроби, поставив запятую после данного числа и записав сколько угодно нулей после нее.
Порядок выполнения действий: если в выражении есть скобки, то сначала выполняют действия в скобках.
№6.228 учебника 2021-2022 (стр. 110):
а) (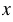 - 7,38) • 4 = 18
- 7,38) • 4 = 18
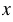 - 7,38 = 18 : 4
- 7,38 = 18 : 4
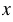 - 7,38 = 4,5
- 7,38 = 4,5
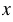 = 4,5 + 7,38
= 4,5 + 7,38
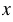 = 11,88
= 11,88
|
|
Ответ: 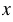 = 11,88.
= 11,88.
б) (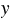 + 0,7) : 3 = 2,69
+ 0,7) : 3 = 2,69
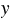 + 0,7 = 2,69 • 3
+ 0,7 = 2,69 • 3
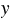 + 0,7 = 8,07
+ 0,7 = 8,07
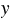 = 8,07 - 0,7
= 8,07 - 0,7
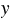 = 7,37
= 7,37
|
|
Ответ: 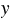 = 7,37.
= 7,37.
Пояснения:
Уравнение - это равенство, содержащее букву, значение которой надо найти. Корень уравнения - это число, которое при подстановке вместо буквы обращает уравнение в верное числовое равенство. Корень уравнения - это решение уравнения. Уравнение может иметь один и более корень или не иметь их вообще. Тогда говорят, что решить уравнение - значит найти все его корни или показать, что их нет вообще.
Для решения уравнений используем:
1) Правило нахождения неизвестного слагаемого: чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.
2) Правило нахождения неизвестного уменьшаемого: чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.
3) Правило нахождения неизвестного множителя: чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.
4) Правило нахождения неизвестного делимого: чтобы найти неизвестное делимое, надо частное умножить на делитель.
а) Рассмотрим уравнение
(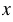 - 7,38) • 4 = 18.
- 7,38) • 4 = 18.
Сначала решаем его относительно умножения, то есть находим неизвестный множитель. Получаем:
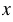 - 7,38 = 18 : 4,
- 7,38 = 18 : 4,
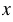 - 7,38 = 4,5.
- 7,38 = 4,5.
Теперь полученное решаем уравнение относительно вычитания, то есть находим неизвестное уменьшаемое. Получаем:
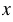 = 4,5 + 7,38,
= 4,5 + 7,38,
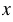 = 11,88.
= 11,88.
б) Рассмотрим уравнение
(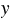 + 0,7) : 3 = 2,69.
+ 0,7) : 3 = 2,69.
Решаем его сначала относительно деления, то есть находим неизвестное делимое. Получаем:
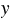 + 0,7 = 2,69 • 3,
+ 0,7 = 2,69 • 3,
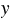 + 0,7 = 8,07.
+ 0,7 = 8,07.
Далее решаем полученное уравнение относительно сложения, то есть находим неизвестное слагаемое. Получаем:
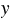 = 8,07 - 0,7,
= 8,07 - 0,7,
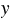 = 7,37.
= 7,37.
Вернуться к содержанию учебника