Задание 6.177 - ГДЗ Математика 5 класс. Виленкин, Жохов. Учебник часть 2. Страница 103
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
№6.177 учебника 2021-2022 (стр. 103):
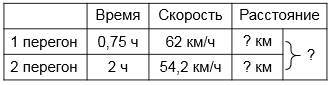
Один перегон электропоезд прошел за 0,75 ч со скоростью 62 км/ч, а другой - за 2 ч со скоростью 54,2 км/ч. Какое расстояние прошел электропоезд за все это время?
Подсказка
№6.177 учебника 2021-2022 (стр. 103):
Вспомните:
- Задачи на движение.
- Умножение десятичных дробей на натуральное число.
- Сложение десятичных дробей.
Ответ
№6.177 учебника 2021-2022 (стр. 103):
1) 62 • 0,75 = 46,5 (км) - длина первого перегона.
| × | 6 | 2 | ||
| 0 | 7 | 5 | ||
| + | 3 | 1 | 0 | |
| 4 | 3 | 4 | ||
| 4 | 6 | 5 | 0 |
2) 54,2 • 2 = 108,4 (км) - длина второго перегона.
| × | 5 | 4 | 2 |
| 2 | |||
| 1 | 0 | 8 | 4 |
3) 46,5 + 108,4 = 154,9 (км)
| + | 1 | 0 | 8 | , | 4 |
| 4 | 6 | , | 5 | ||
| 1 | 5 | 4 | , | 9 |
Ответ: 154,9 км прошел электропоезд.
Пояснения:
Чтобы найти расстояние, нужно скорость движения умножить на время.
Первый перегон электропоезд прошел за 0,75 ч со скоростью 62 км/ч, значит, длина первого перегона:
62 • 0,75 = 46,5 (км).
Второй перегон электропоезд прошел за 2 ч со скоростью 54,2 км/ч, значит, длина второго перегона:
54,2 • 2 = 108,4 (км).
Итак, электропоезд на первом перегоне проехал 46,5 к м , а на втором 108,4 км, значит, за все время электропоезд прошел:
46,5 + 108,4 = 154,9 (км).
Вычисления выполнены по следующим правилам:
1) чтобы умножить десятичную дробь на натуральное число, надо: умножить их как натуральные числа, не обращая внимание на запятую; затем в полученном произведении отделить запятой справа столько цифр, сколько их стоит после запятой у умножаемой дроби;
2) чтобы сложить десятичные дроби, нужно записать числа столбиком так, чтобы запятая стояла под запятой, уравнять в них количество знаков после запятой дописав нули, затем выполнить действие не обращая внимание на запятую, а в ответе поставить запятую под запятой.
Вернуться к содержанию учебника