Задание 2.280 - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 1
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№2.280 учебника 2023-2024 (стр. 82):
Найдите значение  по формуле
по формуле 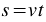 , если:
, если:

№2.280 учебника 2021-2022 (стр. 77):
Найдите значение выражения:

Подсказка
№2.280 учебника 2023-2024 (стр. 82):
Вспомните:
- Вычисления по формулам.
- Смешанные числа.
- Неправильные дроби.
- Умножение смешанных чисел и обыкновенных дробей.
- Сокращение дробей.
- Деление и дроби.
- Деление с остатком.
№2.280 учебника 2021-2022 (стр. 77):
Вспомните:
- Умножение обыкновенных дробей.
- Сокращение дробей.
Ответ
№2.280 учебника 2023-2024 (стр. 82):

Пояснения:
Чтобы найти значение  по формуле
по формуле  , нужно в эту формулу вместо
, нужно в эту формулу вместо  и
и 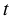 подставить числа, им соответствующие, и выполнить вычисления.
подставить числа, им соответствующие, и выполнить вычисления.
Чтобы выполнить умножение смешанных чисел, нужно записать эти числа в виде неправильных дробей, а затем воспользоваться правилом умножения дробей, согласно которому произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель - произведению знаменателей.
Чтобы преобразовать смешанное число в неправильную дробь, надо целую часть числа умножить на знаменатель дробной части и к полученному произведению прибавить числитель дробной части; эту сумму записать как числитель неправильной дроби, а в ее знаменатель записать знаменатель дробной части смешанного числа.
Чтобы вычисления были проще, не надо перемножать сразу, лучше сделать это после сокращения.
Сократить дробь - значит, разделить ее числитель и знаменатель на одно и то же число (наибольший общий делитель).
Если при вычислениях получилась неправильная дробь, преобразуем ее в смешанное число. Чтобы неправильную дробь, числитель которой нацело не делится на знаменатель, преобразовать в смешанное число, надо числитель разделить на знаменатель; полученное неполное частное записать как целую часть смешанного числа, а остаток - как числитель его дробной части.
№2.280 учебника 2021-2022 (стр. 77):

Пояснения:
Произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель - произведению знаменателей.
Чтобы вычисления были проще, не надо перемножать сразу, лучше сделать это после сокращения.
Сократить дробь - значит, разделить ее числитель и знаменатель на одно и то же число (наибольший общий делитель).
Вернуться к содержанию учебника