Задание 1.23 - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 1
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№1.23 учебника 2023-2024 (стр. 16):
Найдите корень уравнения:
а) 4,1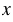 - 2,9
- 2,9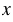 + 7,5 = 7,98;
+ 7,5 = 7,98;
б) 7,8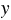 - (5,6
- (5,6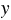 + 10,6) = 3,7;
+ 10,6) = 3,7;
в) (8,3 - 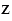 ) • 4,9 = 5,88;
) • 4,9 = 5,88;
г) (11,2 - 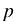 ) • 4,5 = 31,5.
) • 4,5 = 31,5.
№1.23 учебника 2021-2022 (стр. 15):
Используя калькулятор, найдите значение выражения:
а) 56,034 + 4,967;
б) 643,27 - 382,79;
в) 14,27•58,34;
г) 92,41 : 8,123;
д) 407,4 + 9342,528 : 24,7;
е) 84,5•13,6 - 659,45.
Подсказка
№1.23 учебника 2023-2024 (стр. 16):
Вспомните:
- Что называют уравнением, его корни.
- Сложение и вычитание десятичных дробей.
- Деление десятичных дробей.
- Распределительное свойство умножения.
- Свойства вычитания.
№1.23 учебника 2021-2022 (стр. 15):
Вспомните:
- Как выполнять математические операции на калькуляторе.
- Порядок выполнения действий.
Ответ
№1.23 учебника 2023-2024 (стр. 16):
а) 4,1 - 2,9
- 2,9 + 7,5 = 7,98
+ 7,5 = 7,98
(4,1 - 2,9
- 2,9 ) + 7,5 = 7,98
) + 7,5 = 7,98
(4,1 - 2,9) + 7,5 = 7,98
+ 7,5 = 7,98
1,2 + 7,5 = 7,98
+ 7,5 = 7,98
1,2 = 7,98 - 7,5
= 7,98 - 7,5
1,2 = 0,48
= 0,48
 = 0,48 : 1,2
= 0,48 : 1,2
 = 48 : 120
= 48 : 120
 = 0,4
= 0,4
Ответ:  = 0,4.
= 0,4.
б) 7,8 - (5,6
- (5,6 + 10,6) = 3,7
+ 10,6) = 3,7
(7,8 - 5,6
- 5,6 ) - 10,6 = 3,7
) - 10,6 = 3,7
(7,8 - 5,6) - 10,6 = 3,7
- 10,6 = 3,7
2,2 - 10,6 = 3,7
- 10,6 = 3,7
2,2 = 3,7 + 10,6
= 3,7 + 10,6
2,2 = 14,3
= 14,3
 = 14,3 : 2,2
= 14,3 : 2,2
 = 143 : 22
= 143 : 22
 = 6,5
= 6,5
| - | 1 | 4 | 3 | 2 | 2 | ||||||||||
| 1 | 3 | 2 | 6 | , | 5 | ||||||||||
| - | 1 | 1 | 0 | ||||||||||||
| 1 | 1 | 0 | |||||||||||||
| 0 |
Ответ:  = 6,5.
= 6,5.
в) (8,3 - 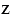 ) • 4,9 = 5,88
) • 4,9 = 5,88
8,3 - 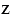 = 5,88 : 4,9
= 5,88 : 4,9
8,3 - 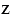 = 58,8 : 49
= 58,8 : 49
8,3 - 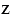 = 1,2
= 1,2
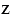 = 8,3 - 1,2
= 8,3 - 1,2
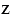 = 7,1
= 7,1
| - | 5 | 8 | 8 | 4 | 9 | ||||||||||
| 4 | 9 | 1 | 2 | ||||||||||||
| - | 9 | 8 | |||||||||||||
| 9 | 8 | ||||||||||||||
| 0 |
Ответ: 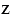 = 7,1.
= 7,1.
г) (11,2 - 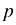 ) • 4,5 = 31,5
) • 4,5 = 31,5
11,2 - 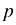 = 31,5 : 4,5
= 31,5 : 4,5
11,2 - 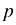 = 315 : 45
= 315 : 45
11,2 - 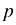 = 7
= 7
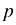 = 11,2 - 7
= 11,2 - 7
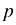 = 4,2
= 4,2
Ответ: 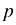 = 4,2.
= 4,2.
Пояснения:
Корень уравнения - это число, которое при подстановке вместо буквы обращает уравнение в верное числовое равенство. Решить уравнение - значит найти все его корни или показать, что их нет вообще.
а) В левой части уравнения
4,1 - 2,9
- 2,9 + 7,5 = 7,98
+ 7,5 = 7,98
сначала применяем сочетательное свойство сложения (группируем слагаемые, содержащие переменные):
(4,1 - 2,9
- 2,9 ) + 7,5 = 7,98.
) + 7,5 = 7,98.
Затем, к выражению, стоящему в скобках, применяем распределительное свойство умножения относительно вычитания (выносим переменную за скобки):
(4,1 - 2,9) + 7,5 = 7,98,
+ 7,5 = 7,98,
1,2 + 7,5 = 7,98.
+ 7,5 = 7,98.
Теперь решаем полученное уравнение относительно сложения, то есть находим неизвестное слагаемое. Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое. Тогда:
1,2 = 7,98 - 7,5,
= 7,98 - 7,5,
1,2 = 0,48.
= 0,48.
Далее решаем уравнение относительно умножения, то есть находим неизвестный множитель. Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель. Тогда:
 = 0,48 : 1,2,
= 0,48 : 1,2,
 = 48 : 120,
= 48 : 120,
 = 0,4.
= 0,4.
б) В левой части уравнения
7,8 - (5,6
- (5,6 + 10,6) = 3,7
+ 10,6) = 3,7
сначала применяем свойство вычитания суммы чисел из числа, согласно которому, чтобы вычесть сумму чисел из числа, можно вычесть из данного числа любое из слагаемых, поле этого вычесть второе. Тогда:
(7,8 - 5,6
- 5,6 ) - 10,6 = 3,7.
) - 10,6 = 3,7.
Затем, к выражению, стоящему в скобках, применяем распределительное свойство умножения относительно вычитания (выносим переменную за скобки):
(7,8 - 5,6) - 10,6 = 3,7,
- 10,6 = 3,7,
2,2 - 10,6 = 3,7.
- 10,6 = 3,7.
Далее полученное уравнение решаем относительно вычитания, то есть находим неизвестное уменьшаемое. Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое, тогда:
2,2 = 3,7 + 10,6,
= 3,7 + 10,6,
2,2 = 14,3.
= 14,3.
Теперь решаем полученное уравнение относительно умножения, то есть находим неизвестный множитель. Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель, тогда:
 = 14,3 : 2,2,
= 14,3 : 2,2,
 = 143 : 22,
= 143 : 22,
 = 6,5.
= 6,5.
в) Уравнение (8,3 - 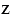 ) • 4,9 = 5,88 сначала решаем относительно умножения, то есть находим неизвестный множитель. Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель, тогда:
) • 4,9 = 5,88 сначала решаем относительно умножения, то есть находим неизвестный множитель. Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель, тогда:
8,3 - 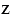 = 5,88 : 4,9,
= 5,88 : 4,9,
8,3 - 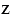 = 58,8 : 49,
= 58,8 : 49,
8,3 - 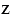 = 1,2.
= 1,2.
Теперь решаем уравнение относительно вычитания, то есть находим неизвестное вычитаемое. Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность, тогда:
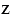 = 8,3 - 1,2,
= 8,3 - 1,2,
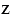 = 7,1.
= 7,1.
г) Уравнение (11,2 - 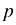 ) • 4,5 = 31,5 решаем по такому же алгоритму как уравнение из пункта в).
) • 4,5 = 31,5 решаем по такому же алгоритму как уравнение из пункта в).
№1.23 учебника 2021-2022 (стр. 15):
а) 56,034 + 4,967 = 61,001;
б) 643,27 - 382,79 = 260,48;
в) 14,27•58,34 = 832,5118;
г) 92,41 : 8,123 = 11,37633879...;
д) 407,4 + 9342,528 : 24,7 = 785,64;
е) 84,5•13,6 - 659,45 = 489,75.
Пояснения:
Числа в калькулятор вводится, начиная со старших разрядов. Чтобы сбросить число с экрана, нажимают клавишу с буквой С (DEL).
Алгоритм выполнения арифметических действий над числами 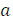 и
и 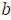 :
:
1) ввести число 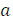 ;
;
2) нажать клавишу выполняемой операции;
3) ввести число 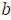 ;
;
4) нажать клавишу со знаком "равно".
Заметим, что если нам дан пример, в котором содержаться несколько действий, то надо выполнять действия, соблюдая порядок, при этом после каждого выполненного действия нажимаем клавишу со знаком "равно".
Рассмотрим последний пример:
1) так как первым действием будем выполнять умножение, сначала вводим число 84,5.
2) нажимаем клавишу ×;
3) вводим число 13,6;
4) нажимаем клавишу =, на экране высветится ответ 1149,2;
5) затем нажимаем клавишу -;
6) вводим число 659,45;
7) нажимаем клавишу =, на экране высветится ответ 489,75.
То есть в итоге получаем, что:
84,5•13,6 - 659,45 = 489,75.
Вернуться к содержанию учебника