Задание 3.218 - ГДЗ Математика 5 класс. Виленкин, Жохов. Учебник часть 1. Страница 102
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№3.218 учебника 2023-2024 (стр. 102):
Площадь класса в 7 раз меньше площади физкультурного зала. Найдите площадь зала, если она больше площади класса на 288 квадратных метров.
№3.218 учебника 2021-2022 (стр. 102):
Площадь класса в 7 раз меньше площади физкультурного зала. Найдите площадь зала, если она больше площади класса на 288 м2.
Подсказка
№3.218 учебника 2023-2024 (стр. 102):
№3.218 учебника 2021-2022 (стр. 102):
Вспомните:
- Что называют уравнением, его корни.
- Свойства умножения.
- Вычитание чисел.
- Деление чисел.
- Буквенные выражения.
Ответ
№3.218 учебника 2023-2024 (стр. 102):
№3.218 учебника 2021-2022 (стр. 102):
Пусть 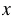 м2 - площадь класса, тогда площадь физкультурного зала 7
м2 - площадь класса, тогда площадь физкультурного зала 7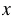 м2. Площадь зала больше площади класса на 288 м2.
м2. Площадь зала больше площади класса на 288 м2.
Получаем уравнение:
7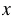 -
- 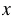 = 288
= 288
6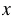 = 288
= 288
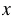 = 288 : 6
= 288 : 6
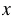 = 48 (м2) - площадь класса.
= 48 (м2) - площадь класса.
| - | 2 | 8 | 8 | 6 | ||||||||||
| 2 | 4 | 4 | 8 | |||||||||||
| - | 4 | 8 | ||||||||||||
| 4 | 8 | |||||||||||||
| 0 |
7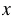 = 7 • 48 = 336 (м2)
= 7 • 48 = 336 (м2)
| × | 4 | 8 |
| 7 | ||
| 3 | 3 | 6 |
Ответ: площадь физкультурного зала равна 336 м2.
Пояснения:
Решаем задачу при помощи уравнения.
Равенство, содержащее неизвестное число, обозначенное буквой называют уравнением.
Корнем уравнения называют значение буквы, при котором уравнение становится верным числовым равенством.
Решить уравнение - значит найти все его корни (или убедиться, что это уравнение не имеет корня).
При решении полученного уравнения сначала в левой его части применяем распределительное свойство умножения относительно вычитания. А затем находим неизвестный множитель.
Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
Вернуться к содержанию учебника