Задание 18. Вопросы для повторения к главе VI - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник. Страница 136
Старая и новая редакции
Вернуться к содержанию учебника
Вопросы для повторения к главе VI. Страница 136
Вопрос
№18 учебника 2023-2024 (стр. 136):
Подсказка
№18 учебника 2023-2024 (стр. 136):
Вспомните:
- Что называют квадратом, признаки квадрата.
- Что называют прямоугольником, его свойства.
- Что называют ромбом, его свойства.
- Какой треугольник называют прямоугольным.
- Признаки равенства прямоугольных треугольников.
- Свойства прямоугольного треугольника.
- Сумма углов четырехугольника.
- Какие прямые называю перпендикулярными.
Ответ
№18 учебника 2023-2024 (стр. 136):
Квадрат – это прямоугольник, у которого все стороны равны.
Признаки квадрата:
1) Если две смежные стороны прямоугольника равны, то этот прямоугольник является квадратом.
Дано: АВСD - прямоугольник, АВ = ВС.
Доказать: АВСD - квадрат.
Доказательство:
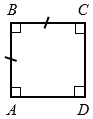
АВСD - прямоугольник, 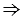 АВ = СD и ВС = АD, при этом АВ = ВС,
АВ = СD и ВС = АD, при этом АВ = ВС, 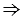
АВ = ВС = СD = АD.
Итак, в четырехугольнике АВСD все стороны равны и все углы прямые, 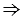 АВСD - квадрат по определению. Что и требовалось доказать.
АВСD - квадрат по определению. Что и требовалось доказать.
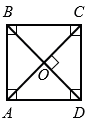
2) Если диагонали прямоугольника перпендикулярны, то этот прямоугольник является квадратом.
Дано: АВСD - прямоугольник, АС ВD.
ВD.
Доказать: АВСD - квадрат:
Доказательство:
В прямоугольных 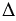 АОВ и
АОВ и  ВОС:
ВОС:
ОА = ОВ = ОС, так как в прямоугольнике диагонали равны и и точкой пересечения делятся пополам, 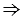
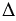 АОВ и
АОВ и 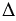 ВОС по двум катетам,
ВОС по двум катетам, 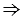 АВ = ВС,
АВ = ВС, 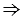 АВСD - квадрат (смотри первый признак квадрата). Что и требовалось доказать.
АВСD - квадрат (смотри первый признак квадрата). Что и требовалось доказать.
3) Если один из углов ромба прямой, то этот ромб является квадратом.
Дано: АВСD - ромб, 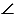 А = 900.
А = 900.
Доказать: АВСD - квадрат:
Доказательство:
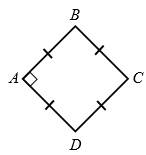
АВСD - ромб, 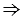
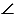 А =
А = 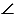 С = 900 и
С = 900 и 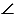 В =
В = 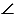 D. Сумма углов четырехугольника равна 3600,
D. Сумма углов четырехугольника равна 3600, 
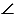 В =
В = 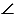 D = (3600 -
D = (3600 - 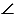 А -
А -  С) : 2 =
С) : 2 =
= (3600 - 900 - 900) : 2 = 1800 : 2 = 900.
Итак, в четырехугольнике АВСD все стороны равны и все углы прямые,  АВСD - квадрат по определению. Что и требовалось доказать.
АВСD - квадрат по определению. Что и требовалось доказать.
4) Если диагонали ромба равны, то этот ромб является квадратом.
Дано: АВСD - ромб, АС = ВD.
Доказать: АВСD - квадрат.
Доказательство:
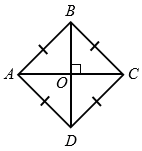
АВСD - ромб, АС
АС 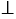 ВD, при этом АС = ВD,
ВD, при этом АС = ВD, 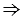 прямоугольный
прямоугольный 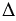 АОВ - равнобедренный,
АОВ - равнобедренный, 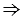
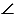 ОАВ =
ОАВ = 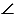 ОВА (как углы при основании равнобедренного треугольника),
ОВА (как углы при основании равнобедренного треугольника), 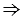
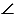 ОАВ =
ОАВ = 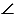 ОВА = 900 : 2 = 450 (свойство прямоугольного треугольника).
ОВА = 900 : 2 = 450 (свойство прямоугольного треугольника).
Аналогично, 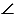 ОВС =
ОВС = 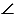 ОСВ = 450,
ОСВ = 450, 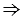
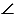 В =
В = 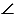 ОВА +
ОВА + 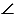 ОВС = 450 + 450 = 900,
ОВС = 450 + 450 = 900, 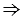 АВСD - квадрат (смотри третий признак квадрата). Что и требовалось доказать.
АВСD - квадрат (смотри третий признак квадрата). Что и требовалось доказать.
Вернуться к содержанию учебника