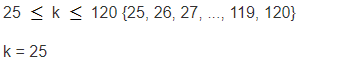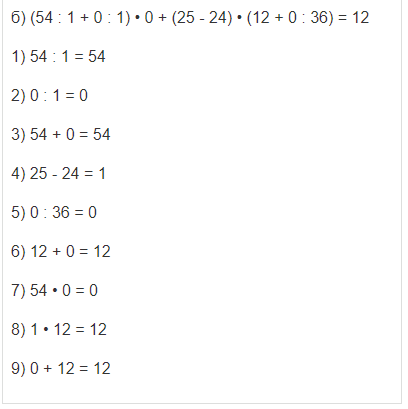Страница 35. Урок 12 - ГДЗ Математика 4 класс. Петерсон. Учебник часть 1
Вернуться к содержанию учебника
Страница 32. Урок 11 Страница 33. Урок 11 Страница 34. Урок 12 Страница 35. Урок 12 Страница 36. Урок 12 Страница 38. Урок 13 Страница 39. Урок 13
Вопрос
Задание № 5. У Марины сегодня день рождения. Она младше своего родного брата, которому неделю назад исполнилось 8 лет. Сколько лет может быть Марине? Составь неравенство и укажи множество его решений.
Подсказка
Повтори, что такое неравенства.
Ответ
Решение
Марина < 8
{1, 2, 3, 4, 5, 6, 7}
Пояснение
Когда какие-нибудь объекты собирают вместе, в математике для их названия используют общее слово - множество.
Вопрос
Задание № 6. Какие из чисел 7, 25, 124, 0 являются решениями данных неравенств?
| х > 65 | 15 + а  45 45 |
| 6 + у < 12 | 7  t < 25 t < 25 |
| 4 • b > 100 | 25  k k  120 120 |
Подсказка
Повтори, что такое неравенства.
Ответ
Вопрос
Задание № 7. Летели галки и сели на палки. Палок было 5. Если галки сядут по одной на каждую палку, то некоторым галкам не хватит места, а если они сядут по две на каждую палку, то некоторые палки останутся свободными. Сколько было галок?
Ответ
Решение
6 или 8
Пояснение
Галок было больше 5, но не больше 10.
Рассмотрим варианты: 6, 7, 8, 9 и 10.
6: Если галки сядут по одной, палок не хватит, если по две, то 2 палки будут свободными.
7: Если галки сядут по одной, палок не хватит, если по две, то одна галка останется без пары, если она сядет одна - это не соответствует условию.
8: Если галки сядут по одной, палок не хватит, если по две, то 1 палка будет свободной.
9: одна галка будет без пары и свободных палок не останется.
10: все палки будут заняты - это не соответствует условию.
Вопрос
Задание № 8. На решение трёх задач Петя потратил а минут. Первую задачу он решал b минут, а вторую - на с минут дольше, чем первую. Сколько времени он решал третью задачу? Составь выражение и найди его значение при а = 25, b = 7, с = 5.
Подсказка
Повтори, что такое буквенные выражения.
Ответ
Решение
а - b - (b + c)
25 - 7 - (7 + 5) = 6 (мин)
Ответ: Петя решал третью задачу 6 мин.
Пояснение
Буквенное выражение, содержащее переменную, называют выражением с переменной.
Вопрос
Задание № 9.
а) Мотоциклист проехал до озера 126 км, а затем ещё 84 км. На весь путь он затратил 5 часов. Сколько времени мотоциклист ехал до озера и сколько потом, если его скорость в пути не изменялась?
б) В одной книге 126 страниц, а в другой - 84 страницы. Толя прочитал обе книги за 5 часов. Сколько времени он читал каждую книгу, если скорость чтения его при этом не изменялось?
Что общего и что различного в этих задачах? Придумай задачи с другими величинами, имеющие такое же решение.
Подсказка
Ответ
Решение
а) 1) 126 + 84 = 210 (км) - весь путь.
2) 210 : 5 = 42 (км/ч) - скорость.
3) 126 : 42 = 3 (ч)
4) 84 : 42 = 2 (ч)
Ответ: 3 ч мотоциклист ехал до озера и 2 ч он ехал потом.
б) 1) 126 + 84 = 210 (стр.) - всего.
2) 210 : 5 = 42 (стр./ч) - скорость чтения.
3) 126 : 42 = 3 (ч)
4) 84 : 42 = 2 (ч)
Ответ: 3 ч он читал первую книгу и 2 ч он читал вторую книгу.
Решение задач одинаковое, а величины в них разные.
Пример 1:
Один груз имеет массу 126 кг, а другой - 84 кг. Его разложили равномерно в 5 ящиков. Сколько ящиков занял первый груз и сколько второй груз?
1) 126 + 84 = 210 (кг) - всего.
2) 210 : 5 = 42 (кг) - в одном ящике.
3) 126 : 42 = 3 (ящ.)
4) 84 : 42 = 2 (ящ.)
Ответ: первый груз занял 3 ящика, второй груз занял 2 ящика.
Пример 2:
Одна бочка имеет объём 126 л, а другая - 84 л. Воду разлили равномерно в 5 сосудов. Сколько сосудов заняла первая бочка и сколько вторая бочка?
1) 126 + 84 = 210 (л) - всего.
2) 210 : 5 = 42 (л) - в одном сосуде.
3) 126 : 42 = 3 (с.)
4) 84 : 42 = 2 (с.)
Ответ: первая бочка заняла 3 сосудов, вторая бочка заняла 2 сосуда.
Пояснение
Скорость равна расстоянию, делённому на время движения.
Вопрос
Задание № 10. Какие свойства 0 и 1 ты знаешь? Запиши их с помощью букв. Составь программу действий и вычисли:
| а) (418 : 418 - 0 • 75) • (62 - 62) + (89 • 1) : 89 |
| б) (54 : 1 + 0 : 1) • 0 + (25 - 24) • (12 + 0 : 36) |
Ответ
Вернуться к содержанию учебника