Задание П.90. Вопросы и задачи на повторение. Задачи - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 2. Страница 134

Точка С(4; 4).

Отрезок DЕ:   D(-5; 5) и Е(-2; -3).

NK DЕ, АР DЕ

Пояснения:

Сначала построим координатную плоскость. Проведем две взаимно перпендикулярные оси. Выбираем на них масштаб, например, при котором 1 клетка будет соответствовать 1 единичному отрезку.

Чтобы отметить точку С(4; 4) в полученной координатной плоскости, нужно пройти от начала отсчета по оси 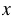вправо на 4 клетки и на 4 клетки вверх.

Чтобы отметить точку D(-5; 5) в полученной координатной плоскости, нужно пройти от начала отсчета по оси 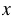влево на 5 клеток и на 5 клеток вверх.

Чтобы отметить точку Е(-2; -3) в полученной координатной плоскости, нужно пройти от начала отсчета по оси 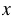влево на 2 клетки и на 3 клетки вниз.

Соединив точки D и Е получим отрезок DЕ.

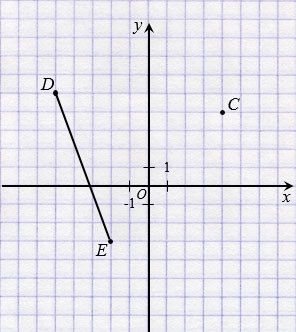
Теперь проведем через точку С прямую NK, перпендикулярную прямой DЕ. Для этого используем чертежный треугольник. Прикладываем чертежный треугольник одной из сторон, образующих прямой угол, к отрезку DЕ так, чтобы точка C лежала около другой стороны чертежного треугольника, образующей прямой угол, и проводим вдоль стороны чертежного треугольника через точку С прямую NK, которая будет перпендикулярна прямой DЕ, то есть NK DЕ.

Теперь проведем через точку С прямую АР, параллельную прямой DЕ. Для этого используем чертежный треугольник. Прикладываем чертежный треугольник одной из сторон, образующих прямой угол, к прямой NK так, чтобы точка C лежала в вершине прямого угла чертежного треугольника, и проводим вдоль другой стороны чертежного треугольника, образующей прямой угол, прямую АР которая будет перпендикулярна прямой NK, а значит, она будет параллельна прямой DЕ, то есть АР NK и АР DЕ (мы использовали то, что две прямые перпендикулярные одной прямой параллельны).