Задание П.89. Вопросы и задачи на повторение. Задачи - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 2. Страница 134

А(-6; -4), В(-2; 6), С(7; 2)

АВ = 5,4 см, ВС = 4,9 см, АС = 7,2 см.

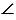А = 43⁰, 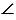В = 88⁰, 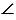С = 49⁰.

М(0,5; -1) - середина стороны АС.

Треугольник АВС - разносторонний, он не обладает симметрией.

Пояснения:

Построим треугольник с вершинами в точках А(-6; -4), В(-2; 6), С(7; 2). Для этого сначала построим координатную плоскость. Проведем две взаимно перпендикулярные оси. Выбираем на них масштаб, например, при котором 1 клетка будет соответствовать 1 единичному отрезку.

Чтобы отметить точку А(-6; -4) в полученной координатной плоскости, нужно пройти от начала отсчета по оси 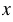влево на 6 клеток и на 4 клетки вниз.

Чтобы отметить точку В(-2; 6) в полученной координатной плоскости, нужно пройти от начала отсчета по оси 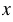влево на 2 клетки и на 6 клеток вверх.

Чтобы отметить точку С(7; 2) в полученной координатной плоскости, нужно пройти от начала отсчета по оси 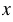вправо на 7 клеток и на 2 клетки вверх.

Соединив последовательно отмеченные точки А, В и С, получаем треугольник АВС.

Теперь с помощью линейки измеряем стороны полученного треугольника АВС, имеем: АВ = 5,4 см, ВС = 4,9 см, АС = 7,2 см.

С помощью транспортира измеряем углы треугольника АВС, имеем:

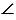А = 43⁰, 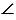В = 88⁰, 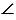С = 49⁰.

Теперь находим середину отрезка АС - точку М (середина делит отрезок пополам).

Опустив из точки М перпендикуляры к осям 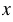и 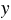определяем координаты точки М, имеем: М(0,5; -1).

Треугольник АВС - разносторонний, следовательно, он не обладает симметрией.