Задание П.55. Вопросы и задачи на повторение. Задачи - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 2. Страница 131

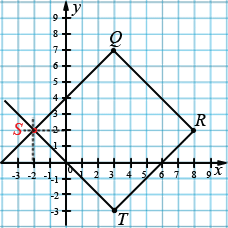
S(-2; 2).

Пояснения:

Чертим прямоугольную систему координат с единичным отрезком 1 клетка.

Отметим в этой системе координат точки  Q(3; 7), R(8; 2) и T(3; -3).

Чтобы попасть в точку Q с координатами (3; 7) , нужно сначала пройти по оси 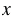от начала отсчета вправо на 3 единицы, а потом - на 7 единиц вверх.

Чтобы попасть в точку R с координатами (8; 2), нужно сначала пройти по оси 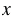от начала отсчета вправо на 8 единиц, а потом - на 2 единицы вверх.

Чтобы попасть в точку T с координатами (3; -3), нужно сначала пройти по оси 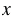от начала отсчета вправо на 3 единицы, а потом - на 3 единицы вниз.

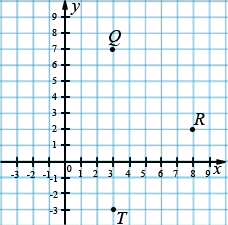
Далее последовательно соединяем точки Q, R, T и получаем две стороны треугольника.

Квадрат - это прямоугольник, у которого все стороны равны. Значит, все его углы прямые. Тогда, чтобы найти четвертую вершину, нам надо провести лучи перпендикулярные сторонам QR и RT с началом в точках Q и T. Для этого помещаем вершину прямого угла треугольника в точку Q, так чтобы одна из сторон прямого угла совпала со стороной QR и проводим луч вдоль другой стороны прямого угла.

Аналогично проводим луч из точки T.

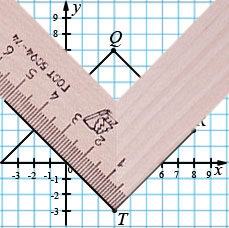
Отмечаем точку пересечения данных лучей, которая будет являться четвертой вершиной S квадрата  QRTS. 

Чтобы определить координаты точки, нужно опустить из этой точки перпендикуляры на ос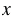и и 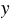, которые и укажут координаты точки.

Значит, точка S имеет координаты

(-2; 2), т.е. S(-2; 2).