Задание 6.61 - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 2. Страница 108

а) А(-1; 6), В(7; -5), С(-3; -3), D(4; 0),

А₁(1; -6), В₁(-7; 5), С₁(3; 3), D₁(-4; 0) - точки симметричные относительно начала координат.

б) А(-1; 6), В(7; -5), С(-3; -3), D(4; 0),

А₁(-1; 6), В₁(7; 5), С₁(-3; 3), D₁(4; 0) - точки симметричные относительно оси абсцисс.

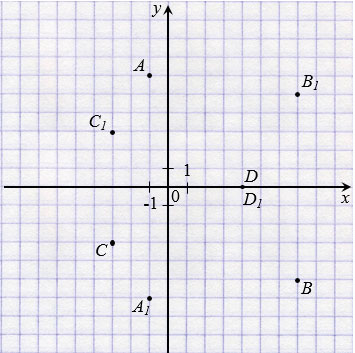
в) А(-1; 6), В(7; -5), С(-3; -3), D(4; 0),

А₁(1; 6), В₁(-7; -5), С₁(3; -3), D₁(-4; 0) - точки симметричные относительно оси ординат.

Пояснения:

Противоположные числа - это числа, которые отличаются только знаками.

а) Две точки координатной плоскости, имеющие противоположные координаты, называют симметричными относительно начала координат.

Значит, точкам

А(-1; 6), В(7; -5), С(-3; -3), D(4; 0)

относительно начала координат симметричны точки

А₁(1; -6), В₁(-7; 5), С₁(3; 3), D₁(-4; 0).

б) Точки координатной плоскости, имеющие одинаковые абсциссы, но противоположные ординаты, называют симметричными относительно оси абсцисс или или, другими словами, симметричными относительно оси  .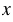

Значит, точкам

А(-1; 6), В(7; -5), С(-3; -3), D(4; 0)

относительно оси абсцисс симметричны точки

А₁(-1; 6), В₁(7; 5), С₁(-3; 3), D₁(4; 0).

в) Точки координатной плоскости, имеющие противоположные абсциссы и одинаковые ординаты, называют симметричными относительно оси ординат или, другими словами, симметричными относительно оси .

Значит, точкам

А(-1; 6), В(7; -5), С(-3; -3), D(4; 0)

относительно оси ординат симметричны точки

А₁(1; 6), В₁(-7; -5), С₁(3; -3), D₁(-4; 0).