Задание 6.58 - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 2. Страница 107

А(2; 5) и В(-2; -5)

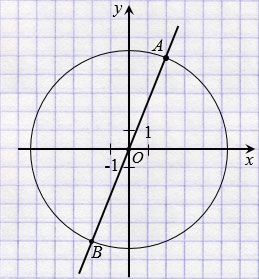
Точки А, В и О лежат на одной прямой.

ОА = ОВ - верно.

Пояснения:

Чертим прямоугольную систему координат с единичным отрезком 1 клетка. Отмечаем в этой системе координат точку А(2; 5) и точку В с противоположными координатами. Противоположные числа отличаются только знаками, значит, В(-2; -5).

Чтобы попасть в точку А с координатами (2; 5), нужно сначала пройти по оси 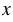от начала отсчета вправо на 2 единицы, а потом - на 5 единиц вверх.

Чтобы попасть в точку В с координатами (-2; -5), нужно сначала пройти по оси 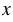от начала отсчета влево на 2 единицы, а потом - на 5 единиц вниз.

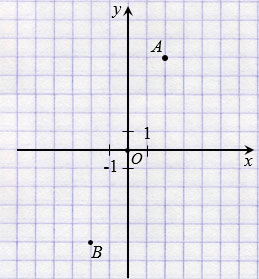
С помощью линейки устанавливаем, что точки А, В и О (начало координат) лежат на одной прямой.

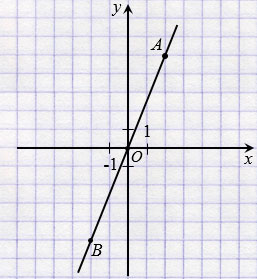
Далее с помощью циркуля устанавливаем то, что ОА = ОВ, так как ОА и ОВ радиусы окружности с центром О, а все радиусы окружности равны.