Задание 6.6 - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 2. Страница 99
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
№6.6 учебника 2021-2022 (стр. 99):
Начертите четырехугольник МNPK, у которого:
а) МN 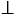 NP;
NP;
б) MN 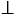 MK и NP
MK и NP 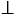 MN;
MN;
в) MN 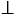 NP, MN
NP, MN 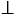 MK и PK
MK и PK 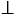 NP.
NP.
Подсказка
№6.6 учебника 2021-2022 (стр. 99):
Вспомните:
- Что называют четырехугольником.
- Перпендикулярные прямые.
Ответ
№6.6 учебника 2021-2022 (стр. 99):
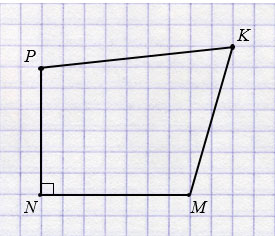
а) МNPK - четырехугольник, у которого МN  NP.
NP.
б) МNPK - четырехугольник, у которого MN  MK и NP
MK и NP  MN.
MN.

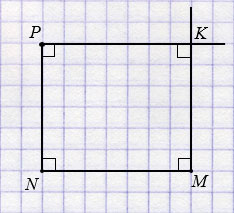
в) МNPK - четырехугольник, у которого MN  NP, MN
NP, MN  MK и PK
MK и PK  NP.
NP.
Пояснения:
а) Чтобы начертить четырехугольник МNPK, у которого МN  NP, Чертим отрезок МN, к отрезку МN прикладываем чертежный треугольник так, чтобы отрезок МN лежал вдоль одной из сторон чертежного треугольника, образующей прямой угол, а точка N лежала в вершине прямого угла чертежного треугольника и проводим перпендикуляр МP к отрезку МN вдоль второй стороны чертежного треугольника, образующей прямой угол, то есть получаем
NP, Чертим отрезок МN, к отрезку МN прикладываем чертежный треугольник так, чтобы отрезок МN лежал вдоль одной из сторон чертежного треугольника, образующей прямой угол, а точка N лежала в вершине прямого угла чертежного треугольника и проводим перпендикуляр МP к отрезку МN вдоль второй стороны чертежного треугольника, образующей прямой угол, то есть получаем
МN NP.
NP.
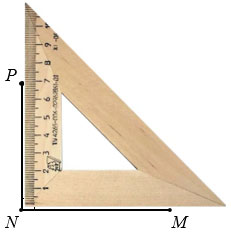
Далее произвольно отмечаем точку K и получаем четырехугольник МNPK, у которого МN  NP.
NP.

б) Чтобы начертить четырехугольник МNPK, у которого MN MK и NP
MK и NP MN. Сначала также как описано в пункте а) чертим МР
MN. Сначала также как описано в пункте а) чертим МР  МN.
МN.

Далее аналогично чертим MN  MK.
MK.

Соединяем точки Р и K и получаем четырехугольник МNPK, у которого
MN  MK и NP
MK и NP  MN.
MN.

в) Чтобы начертить четырехугольник МNPK, у которого MN  NP, MN
NP, MN  MK и PK
MK и PK  NP. Сначала также как описано в пункте а) чертим МР
NP. Сначала также как описано в пункте а) чертим МР  МN.
МN.

Далее аналогично чертим прямую перпендикулярную отрезку NР, проходящую через точку Р.

Теперь аналогично чертим прямую перпендикулярную отрезку МN, проходящую через точку М.
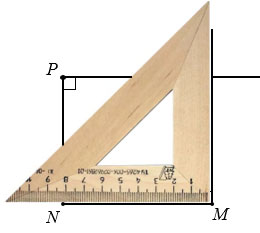
Точку пересечения прямых перпендикулярных к прямым NP и МN обозначаем буквой K и получаем четырехугольник МNPK, у которого
MN  NP, MN
NP, MN  MK и PK
MK и PK  NP.
NP.

Вернуться к содержанию учебника