Задание 6.60 - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 2. Страница 107
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
№6.60 учебника 2023-2024 (стр. 107):
Отметьте на координатной плоскости точки Т и Е, имеющие одинаковые абсциссы, но противоположные ординаты. Проверьте, верно ли, что ТЕ 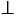 ОА и АТ = АЕ, где О - начало координат, А - точка пересечения ТЕ с осью абсцисс.
ОА и АТ = АЕ, где О - начало координат, А - точка пересечения ТЕ с осью абсцисс.
Точки координатной плоскости, имеющие одинаковые абсциссы, но противоположные ординаты, называют симметричными относительно оси абсцисс.
Подсказка
№6.60 учебника 2023-2024 (стр. 107):
Вспомните:
- Положение точек на координатной плоскости.
- Противоположные числа.
- Перпендикулярные прямые.
- Модуль числа.
Ответ
№6.60 учебника 2023-2024 (стр. 107):
Т(3; 4) и Е(3; -4).

ТЕ 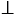 ОА - верно.
ОА - верно.
АТ = АЕ - верно, так как координаты точек Т и Е имеют противоположные ординаты, которые определяют расстояние от оси 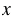 до точек Т и Е, а модули противоположных чисел равны.
до точек Т и Е, а модули противоположных чисел равны.
Пояснения:
Чертим прямоугольную систему координат с единичным отрезком 1 клетка. Отмечаем в этой системе координат точки Т и Е, имеющие одинаковые абсциссы (координаты 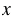 ), но противоположные ординаты (координаты
), но противоположные ординаты (координаты 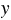 ). Пусть Т(3; 4), тогда Е(3; -4), так как противоположные числа отличаются только знаками.
). Пусть Т(3; 4), тогда Е(3; -4), так как противоположные числа отличаются только знаками.
Чтобы попасть в точку Т с координатами (3; 4), нужно сначала пройти по оси 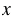 от начала отсчета вправо на 3 единицы, а потом - на 4 единицы вверх.
от начала отсчета вправо на 3 единицы, а потом - на 4 единицы вверх.
Чтобы попасть в точку Е с координатами (3; -4), нужно сначала пройти по оси 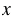 от начала отсчета вправо на 3 единицы, а потом - на 4 единицы вниз.
от начала отсчета вправо на 3 единицы, а потом - на 4 единицы вниз.

Проводим отрезок ТЕ. Обозначаем точку пересечения отрезка ТЕ с осью 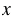 буквой А.
буквой А.

С помощью чертежного треугольника убеждаемся в том, что отрезок ТЕ перпендикулярен ОА, то есть
ТЕ 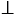 ОА.
ОА.

Утверждение о том, что АТ = АЕ - верно, так как координаты точек Т и Е имеют противоположные ординаты, которые определяют расстояние от оси 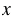 до точек Т и Е, а модули противоположных чисел равны.
до точек Т и Е, а модули противоположных чисел равны.
Вернуться к содержанию учебника