Задание 6.363 - ГДЗ Математика 5 класс. Виленкин, Жохов. Учебник часть 2
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№6.363 учебника 2023-2024 (стр. 141):
Деревянная доска массой 5,25 кг имеет объем 10,5 дм3. Другая доска из этой же древесины имеет объем 6,14 дм3. Чему равна масса второй доски?
№6.363 учебника 2021-2022 (стр. 125):
Найдите корень уравнения:
а) 2,442 : (6,8 -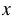 
) = 8,14;
б) 3,6(1,3 +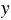 
) = 7,56;
в) 0,3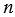
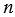+ 1,6 - 0,31 = 0,45;
г) 8,3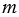
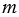- 4 - 1,8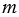 + 4,25 = 8.
Подсказка
№6.363 учебника 2023-2024 (стр. 141):
№6.363 учебника 2021-2022 (стр. 125):
Вспомните:
- Что называют уравнением, его корни.
- Сложение и вычитание десятичных дробей.
- Умножение десятичных дробей (распределительное свойство).
- Деление десятичных дробей.
Ответ
№6.363 учебника 2023-2024 (стр. 141):
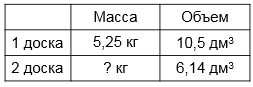
1) 5,25 : 10,5 = 52,5 : 105 = 0,5 (кг) - масса 1 дм3 доски.
| - | 5 | 2 | 5 | 1 | 0 | 5 | |||||||||
| 5 | 2 | 5 | 0 | 5 | |||||||||||
| 0 |
2) 6,14 • 0,5 = 3,07 (кг)
| × | 6 | 1 | 4 |
| 0 | 5 | ||
| 3 | 0 | 7 | 0 |
Ответ: масса второй доски 3,07 кг.
Пояснения:
Чтобы найти массу 1 дм3 доски, нужно массу доски разделить на ее объем.
Деревянная доска массой 5,25 кг имеет объем 10,5 дм3. Значит, масса 1 дм3 доски равна:
5,25 : 10,5 = 52,5 : 105 = 0,5 (кг).
Чтобы найти массу доски нужно массу 1 дм3 доски умножить на ее объем.
Масса 1 дм3 доски 0,5 кг, значит, масса доски объемом 6,14 дм3 равна:
6,14 • 0,5 = 3,07 (кг).
Правила вычислений с десятичными дробями смотрите в подсказке.
№6.363 учебника 2021-2022 (стр. 125):
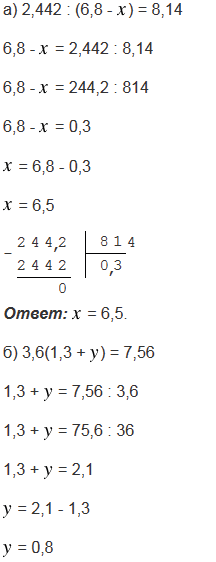
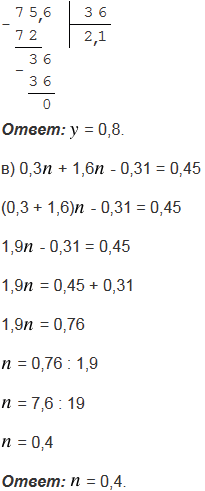
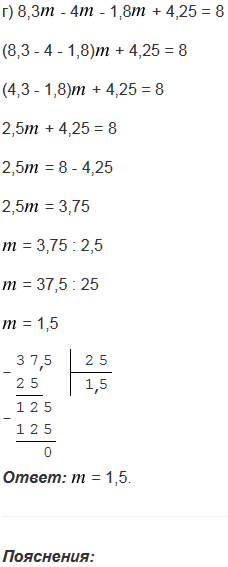
Вернуться к содержанию учебника