Задание 6.153 - ГДЗ Математика 5 класс. Виленкин, Жохов. Учебник часть 2. Страница 99

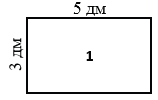
Р₁ = 2$·$(5 + 3) = 2$·$8 = 16 (дм),

S₁ = 3$·$5 = 15 (дм²).

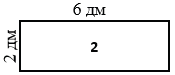
Р₂ = 2$·$(2 + 6) = 2$·$8 = 16 (дм),

S₂ = 2$·$6 = 12 (дм²).

S₁ 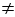S₂.

Ответ: утверждение неверно.

Пояснения:

Пусть мы имеем два участка прямоугольной формы: первый участок со сторонами 5 дм и 3 дм, второй участок со сторонами 6 дм и 2 дм. Чтобы найти периметр прямоугольника, нужно найти удвоенную сумму его соседних сторон. При вычислении периметров (длины забора) первого и второго прямоугольников получим, что их периметры:

Р₁ = 2$·$(5 + 3) = 2$·$8 = 16 (дм);

Р₂ = 2$·$(2 + 6) = 2$·$8 = 16 (дм).

Площадь прямоугольника равна произведению его соседних сторон. Тогда площадь первого прямоугольника

S₁ = 3$·$5 = 15 (дм²),

а площадь второго прямоугольника

S₂ = 2$·$6 = 12 (дм²), т.е. площади первого и второго участков не равны.

Итак, мы получили, что два участка прямоугольной формы имеют одинаковый периметр (длину забора), но разные площади. Следовательно, утверждение "Площади участков, заборы у которых одинаковой длины, равны" - неверно.