Задание 4.141 - ГДЗ Математика 5 класс. Виленкин, Жохов. Учебник часть 1. Страница 149
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
№4.141 учебника 2023-2024 (стр. 149):
№4.141 учебника 2021-2022 (стр. 149):
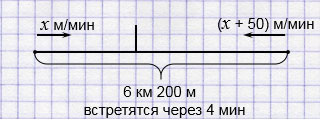
1) С двух станций метро навстречу друг другу движутся два поезда, и скорость одного из них на 50 м/мин меньше скорости другого. Сейчас расстояние между ними 6 км 200 м. Найдите скорость каждого поезда, если известно, что они прибудут на одну станцию через 4 мин.
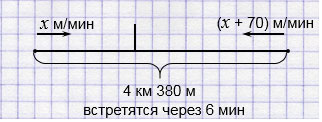
2) Два катера, двигаясь навстречу друг другу, должны встретиться через 6 мин. Сейчас расстояние между ними 4 км 380 м. Найдите скорости этих катеров, если известно, что скорость первого на 70 м/мин меньше скорости второго.
Подсказка
№4.141 учебника 2023-2024 (стр. 149):
№4.141 учебника 2021-2022 (стр. 149):
Вспомните:
- Задачи на движение.
- Что называют уравнением, его корни.
- Умножение чисел, его свойства.
- Деление чисел.
- Вычитание чисел.
- Единицы измерения длины.
Ответ
№4.141 учебника 2023-2024 (стр. 149):
№4.141 учебника 2021-2022 (стр. 149):
1)
Пусть  м/мин скорость первого поезда, тогда (
м/мин скорость первого поезда, тогда ( + 50) м/мин скорость второго поезда, значит, скорость сближения поездов
+ 50) м/мин скорость второго поезда, значит, скорость сближения поездов
 + (
+ ( + 50) = 2
+ 50) = 2 + 50 (км/ч).
+ 50 (км/ч).
Расстояние между поездами
6 км 200 м = 6200 м.
Встреча через 4 мин. Составим уравнение:
(2 + 50) • 4 = 6200
+ 50) • 4 = 6200
2 + 50 = 6200 : 4
+ 50 = 6200 : 4
2 + 50 = 1550
+ 50 = 1550
2 = 1550 - 50
= 1550 - 50
2 = 1500
= 1500
 = 1500 : 2
= 1500 : 2
 = 750 (м/мин) - скорость первого поезда.
= 750 (м/мин) - скорость первого поезда.
|
|
 + 50 = 750 + 50 = 800 (м/мин) - скорость второго поезда.
+ 50 = 750 + 50 = 800 (м/мин) - скорость второго поезда.
Ответ: 750 м/мин и 800 м/мин.
2)
Пусть  м/мин скорость первого катера, тогда (
м/мин скорость первого катера, тогда ( + 70) м/мин скорость второго катера, тогда скорость сближения катеров
+ 70) м/мин скорость второго катера, тогда скорость сближения катеров
 + (
+ ( + 70) = 2
+ 70) = 2 + 70 (км/ч).
+ 70 (км/ч).
Расстояние между катерами
4 км 380 м = 4380 м.
Встреча через 6 мин. Составим уравнение:
(2 + 70) • 6 = 4380
+ 70) • 6 = 4380
2 + 70 = 4380 : 6
+ 70 = 4380 : 6
2 + 70 = 730
+ 70 = 730
2 = 730 - 70
= 730 - 70
2 = 660
= 660
 = 660 : 2
= 660 : 2
 = 330 (м/мин) - скорость первого катера.
= 330 (м/мин) - скорость первого катера.
 + 70 = 330 + 70 = 400 (м/мин) - скорость второго катера.
+ 70 = 330 + 70 = 400 (м/мин) - скорость второго катера.
Ответ: 330 м/мин и 400 м/мин.
Пояснения:
1) Решаем задачу с помощью уравнения.
Равенство, содержащее неизвестное число, обозначенное буквой называют уравнением.
Корнем уравнения называют значение буквы, при котором уравнение становится верным числовым равенством.
Решить уравнение - значит найти все его корни (или убедиться, что это уравнение не имеет корня).
Сначала вводим обозначения.
С двух станций метро навстречу друг другу движутся два поезда, и скорость одного из них на 50 м/мин меньше скорости другого. Пусть  м/мин скорость первого поезда, тогда скорость второго поезда будет равна (
м/мин скорость первого поезда, тогда скорость второго поезда будет равна ( + 50) м/мин, значит, скорость сближения поездов
+ 50) м/мин, значит, скорость сближения поездов
 + (
+ ( + 50) = 2
+ 50) = 2 + 50 (км/ч).
+ 50 (км/ч).
Расстояние между поездами
6 км 200 м = 6200 м, учитываем то, что
1 км = 1000 м (расстояние переводим в метры, так как скорость дана в метрах в минуту).
Поезда прибудут на одну станцию через 4 мин.
Составим уравнение, учитывая то, что, умножив скорость и время, получим расстояние:
(2 + 50) • 4 = 6200.
+ 50) • 4 = 6200.
Полученное уравнение сначала решаем относительно умножения, то есть находим неизвестный множитель 2 + 50:
+ 50:
2 + 50 = 6200 : 4,
+ 50 = 6200 : 4,
2 + 50 = 1550.
+ 50 = 1550.
Далее уравнение решаем относительно сложения, то есть находим неизвестное слагаемое 2 :
:
2 = 1550 - 50,
= 1550 - 50,
2 = 1500.
= 1500.
Теперь снова решаем уравнение относительно умножения, то есть находим неизвестный множитель  :
:
 = 1500 : 2,
= 1500 : 2,
 = 750.
= 750.
Значит, скорость первого поезда равна 750 м/мин. Тогда скорость второго поезда равна:
 + 50 = 750 + 50 = 800 (м/мин) .
+ 50 = 750 + 50 = 800 (м/мин) .
2) Рассуждения проводим также как и в первой задаче.
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
Вернуться к содержанию учебника