Задание 4.101 - ГДЗ Математика 5 класс. Виленкин, Жохов. Учебник часть 1. Страница 144
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№4.101 учебника 2023-2024 (стр. 144):
Прямоугольник МNРK разбит на два треугольника (рис. 4.14). Найдите площадь треугольника KPN, если:
а) MN = 6 м 75 см, МK = 64 м;
б) МN = 9 дм 5 см, МK = 15 дм 8 см.

№4.101 учебника 2021-2022 (стр. 144):
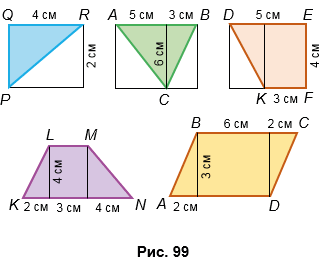
На рисунке 99 изображены фигуры. Найдите их площади.
Подсказка
№4.101 учебника 2023-2024 (стр. 144):
Вспомните:
- Как найти площадь прямоугольника.
- Что называют треугольником.
- Какие фигуры называют равными.
- Свойства площадей.
- Единицы измерения длины.
- Умножение чисел.
- Деление чисел.
№4.101 учебника 2021-2022 (стр. 144):
Вспомните:
- Как найти площадь прямоугольника.
- Что называют треугольником.
- Какие фигуры называют равными.
- Умножение чисел.
- Деление чисел.
Ответ
№4.101 учебника 2023-2024 (стр. 144):
а) MN = 6 м 75 см = 675 см,
МK = 64 м = 6400 см
1) 675 • 6400 = 4 320 000 (см2) =
= 432 (м2) - площадь прямоугольника МNРK .
| × | 6 | 7 | 5 | ||||
| 6 | 4 | 0 | 0 | ||||
| + | 2 | 7 | 0 | 0 | |||
| 4 | 0 | 5 | 0 | ||||
| 4 | 3 | 2 | 0 | 0 | 0 | 0 |
2) 432 : 2 = 216 (м2) - площадь треугольника KPN .
Ответ: 216 м2.
б) МN = 9 дм 5 см = 95 см,
МK = 15 дм 8 см = 158 см.
1) 158 • 95 = 15 010 (см2) - площадь прямоугольника МNРK.
| × | 1 | 5 | 8 | ||
| 9 | 5 | ||||
| + | 7 | 9 | 0 | ||
| 1 | 4 | 2 | 2 | ||
| 1 | 5 | 0 | 1 | 0 |
2) 15 010 : 2 = 7505 (см2) - площадь треугольника KPN.
| - | 1 | 5 | 0 | 1 | 0 | 2 | ||||||||||||
| 1 | 4 | 7 | 5 | 0 | 5 | |||||||||||||
| - | 1 | 0 | ||||||||||||||||
| 1 | 0 | |||||||||||||||||
| - | 1 | 0 | ||||||||||||||||
| 1 | 0 | |||||||||||||||||
| 0 |
Ответ: 7505 см2.
Пояснения:
Чтобы найти площадь треугольника KPN, нужно найти площадь прямоугольника МNРK и разделить эту площадь на 2.
Площадь прямоугольника равна произведению его длины и ширины.
При выполнении вычислений длины сторон нужно привести к одним единицам измерения, при этом учитываем то, что:
1 м = 100 см, 1 дм = 10 см.
1 м2 = 10 000 см2.
№4.101 учебника 2021-2022 (стр. 144):
1) SPQR = (2 • 4) : 2 = 8 : 2 = 4 (см2)
2) SABC = (5 • 6) : 2 + (3 • 6) : 2 =
= 30 : 2 + 18 : 2 = 15 + 9 = 24 (см2)
3) 5 - 3 = 2 (см) - сторона левого прямоугольника.
SDEFK = (2 • 4) : 2 + 3 • 4 = 8 : 2 + 12 =
= 4 + 12 = 16 (см2).
4) SKLMN = (2 • 4) : 2 + 3 • 4 + (4 • 4) : 2 =
= 8 : 2 + 12 + 16 : 2 = 4 + 12 + 8 =
= 24 (см2).
5) SKLMN = 2 • 3 + 3 • 6 = 6 + 18 = 24(см2).
Пояснения:
Чтобы найти площади данных фигур, разбиваем их на треугольники и прямоугольники, находим площади полученных прямоугольников и треугольников, и складываем их (учитываем свойство площадей, согласно которому площадь фигуры равна сумме площадей фигур, из которых она составлена).
Площадь прямоугольника равна произведению его длины и ширины.
Чтобы найти площади треугольников, нужно найти площади прямоугольников, частью которых являются эти треугольники, и разделить их на 2.
Вернуться к содержанию учебника