Задание 3.340 - ГДЗ Математика 5 класс. Виленкин, Жохов. Учебник часть 1. Страница 119
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№3.340 учебника 2023-2024 (стр. 119):
Напишите все делители чисел 8, 15, 26, 23. Какое из них простое? Разложите эти числа на множители.
№3.340 учебника 2021-2022 (стр. 119):
Выпишите из чисел 2, 3, 7, 8, 10, 12, 15, 16, 24, 25 те, которые являются:
а) кратными 6;
б) делителями 24;
в) кратными 5 и делителями 20;
г) делителями 12 и кратными 4.
Подсказка
№3.340 учебника 2023-2024 (стр. 119):
Вспомните:
- Делители и кратные.
- Умножение чисел.
№3.340 учебника 2021-2022 (стр. 119):
Вспомните делители и кратные.
Ответ
№3.340 учебника 2023-2024 (стр. 119):
Делители 8:
1, 2, 4, 8.
8 = 2 • 4 = 1 • 8 = 2 • 2 • 2
Делители 15:
1, 3, 5, 15.
15 = 1 • 15 = 3 • 5.
Делители 26:
1, 2, 13, 26.
26 = 1 • 26 = 2 • 13.
Делители 23:
1, 23.
23 = 1 • 23.
Ответ: простое число - 23.
Пояснения:
Натуральное число 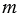 делится без остатка на натуральное число
делится без остатка на натуральное число 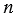 , если есть такое число
, если есть такое число 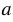 , что
, что 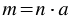 . Натуральное число
. Натуральное число 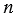 называют делителем натурального числа
называют делителем натурального числа 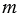 , а число
, а число 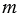 - кратным числа
- кратным числа 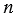 .
.
Натуральное число называют простым, если оно имеет только два делителя: единицу и само это число.
Натуральное число, у которого более двух делителей называют составным.
Единица не является ни простым, ни составным числом.
Разложить число на множители, значит, представить это число в виде произведения двух или более множителей.
№3.340 учебника 2021-2022 (стр. 119):
а) кратными 6:
12, 24.
б) делителями 24:
2, 3, 8, 12, 24.
в) кратными 5 и делителями 20:
10.
г) делителями 12 и кратными 4:
12.
Пояснения:
Натуральное число 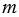 делится без остатка на натуральное число
делится без остатка на натуральное число 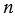 , если есть такое число
, если есть такое число 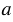 , что
, что 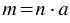 . Натуральное число
. Натуральное число 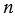 называют делителем натурального числа
называют делителем натурального числа 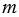 , а число
, а число 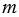 - кратным числа
- кратным числа 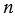 .
.
Натуральное число называют простым, если оно имеет только два делителя: единицу и само это число.
Натуральное число, у которого более двух делителей называют составным.
Единица не является ни простым, ни составным числом.
Вернуться к содержанию учебника