Задание 108 - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник. Страница 37
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№108 учебника 2013-2022 (стр. 37):
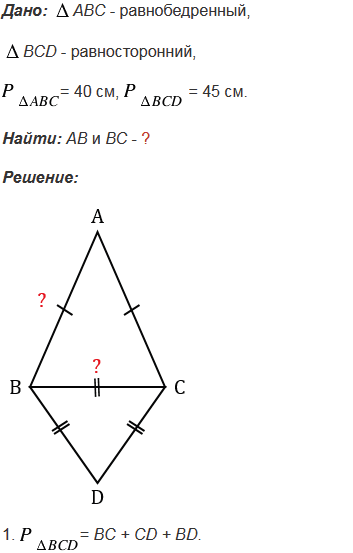
Периметр равнобедренного треугольника АВС с основанием ВС равен 40 см, а периметр равностороннего треугольника ВСD равен 45 см. Найдите стороны АВ и ВС.
№108 учебника 2023-2024 (стр. 37):
Начертите треугольник АВС с тремя острыми углами и треугольник МNP, у которого угол М тупой. С помощью чертежного угольника проведите высоты каждого треугольника.
Подсказка
№108 учебника 2013-2022 (стр. 37):
Вспомните:
- Какой треугольник называется равнобедренным, а какой равносторонним.
- Что такое периметр треугольника.
№108 учебника 2023-2024 (стр. 37):
Вспомните:
- Что такое треугольник.
- Какой угол называется острым, какой тупым.
- Что такое высота треугольника.
Ниже представлены два ответа:
1) для остроугольного треугольника;
2) для тупоугольного треугольника.
Ответ
№108 учебника 2013-2022 (стр. 37):
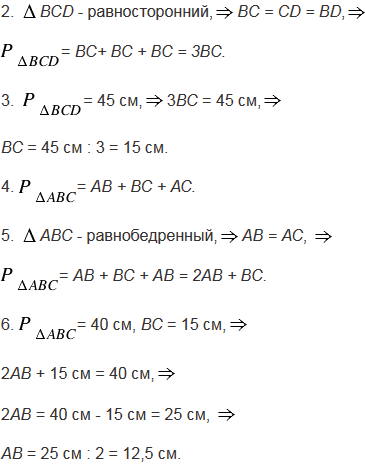



№108 учебника 2023-2024 (стр. 37):
Остроугольный треугольник
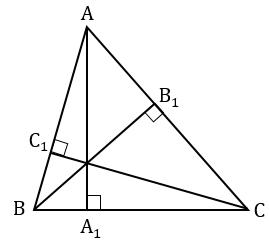
АВС - остроугольный треугольник, АА1, ВВ1, СС1 - высоты  АВС.
АВС.
Пояснения:
Строим треугольник АВС с помощью линейки так, что все его углы острые, т.е. меньше 900.
Чтобы провести высоту 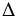 АВС из вершины А к стороне ВС, берем чертежный угольник, прикладываем его так, что одна из его сторон, образующих прямой угол угольника, располагалась вдоль стороны ВС. Вторую сторону угольника, образующую прямой угол, располагаем так, что вершина А лежит вдоль этой стороны.
АВС из вершины А к стороне ВС, берем чертежный угольник, прикладываем его так, что одна из его сторон, образующих прямой угол угольника, располагалась вдоль стороны ВС. Вторую сторону угольника, образующую прямой угол, располагаем так, что вершина А лежит вдоль этой стороны.
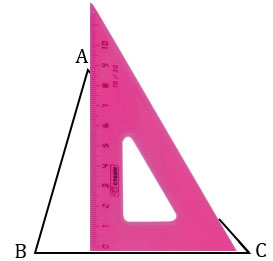
Далее из вершины А проводим прямую вдоль стороны угольника к стороне ВС треугольника АВС.
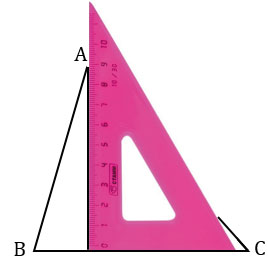
Точку пересечения проведенной прямой со стороной ВС обозначаем А1. Получаем АА1 - высота треугольника АВС, проведенная к стороне ВС.
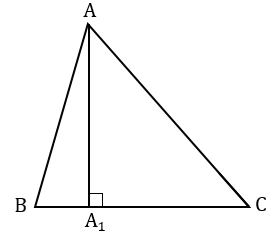
Чтобы провести высоту 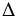 АВС из вершины В к стороне АС, берем чертежный угольник, прикладываем его так, что одна из его сторон, образующих прямой угол угольника, располагалась вдоль стороны АС. Вторую сторону угольника, образующую прямой угол, располагаем так, что вершина В лежит вдоль этой стороны.
АВС из вершины В к стороне АС, берем чертежный угольник, прикладываем его так, что одна из его сторон, образующих прямой угол угольника, располагалась вдоль стороны АС. Вторую сторону угольника, образующую прямой угол, располагаем так, что вершина В лежит вдоль этой стороны.
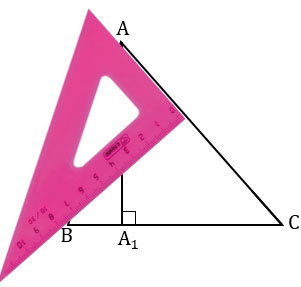
Далее из вершины В проводим прямую вдоль стороны угольника к стороне АС треугольника АВС.
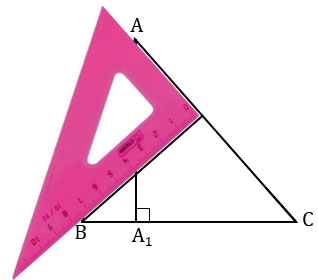
Точку пересечения проведенной прямой со стороной АС обозначаем В1. Получаем ВВ1 - высота треугольника АВС, проведенная к стороне АС.
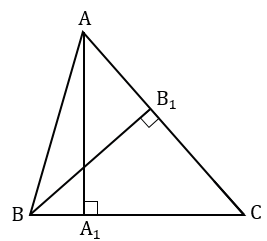
Чтобы провести высоту 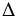 АВС из вершины С к стороне АВ, берем чертежный угольник, прикладываем его так, что одна из его сторон, образующих прямой угол угольника, располагалась вдоль стороны АВ. Вторую сторону угольника, образующую прямой угол, располагаем так, что вершина С лежит вдоль этой стороны.
АВС из вершины С к стороне АВ, берем чертежный угольник, прикладываем его так, что одна из его сторон, образующих прямой угол угольника, располагалась вдоль стороны АВ. Вторую сторону угольника, образующую прямой угол, располагаем так, что вершина С лежит вдоль этой стороны.
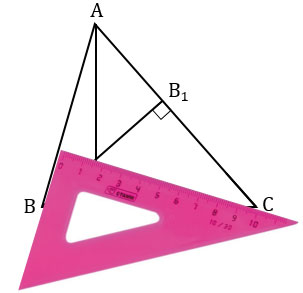
Далее из вершины С проводим прямую вдоль стороны угольника к стороне АВ треугольника АВС.
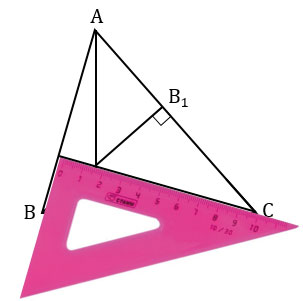
Точку пересечения проведенной прямой со стороной АВ обозначаем С1. Получаем СС1 - высота треугольника АВС, проведенная к стороне АВ.

Тупоугольный треугольник
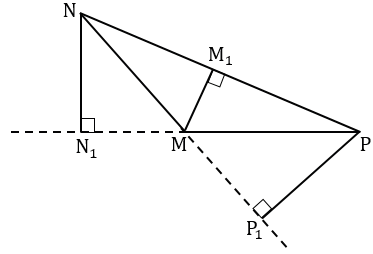
МNР - тупоугольный треугольник,  М - тупой, NN1, ММ1, РР1 - высоты
М - тупой, NN1, ММ1, РР1 - высоты  МNР.
МNР.
Пояснения:
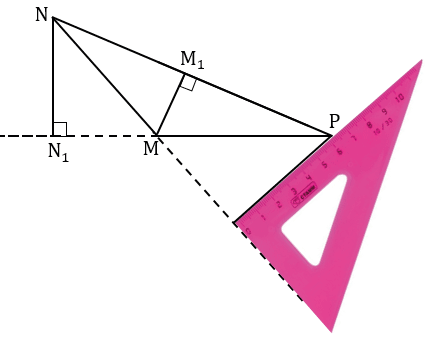
Чтобы провести высоту  MNP из вершины N к стороне MP, берем чертежный угольник, прикладываем его так, что одна из его сторон, образующих прямой угол угольника, располагалась вдоль продолжения стороны МР. Вторую сторону угольника, образующую прямой угол, располагаем так, что вершина N лежит вдоль этой стороны.
MNP из вершины N к стороне MP, берем чертежный угольник, прикладываем его так, что одна из его сторон, образующих прямой угол угольника, располагалась вдоль продолжения стороны МР. Вторую сторону угольника, образующую прямой угол, располагаем так, что вершина N лежит вдоль этой стороны.
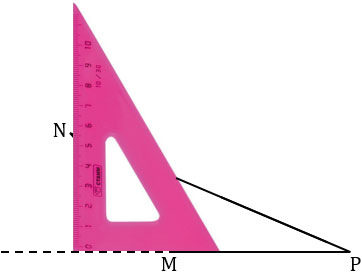
Далее из вершины N проводим прямую вдоль стороны угольника к продолжению стороны MP треугольника MNP.
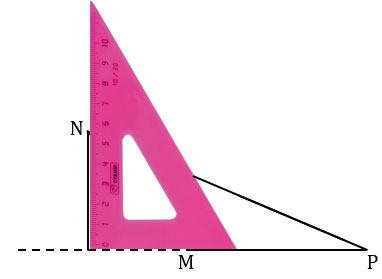
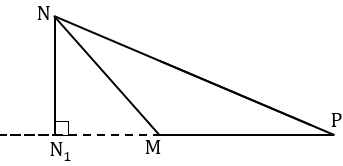
Точку пересечения проведенной прямой с продолжением стороны МР обозначаем N1. Получаем NN1 - высота треугольника MNP, проведенная к стороне MP.
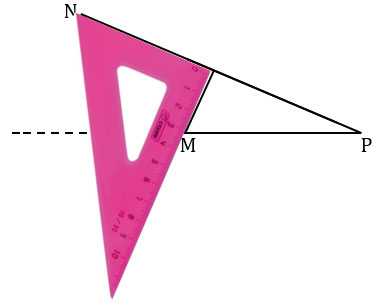
Чтобы провести высоту  MNP из вершины M к стороне NP, берем чертежный угольник, прикладываем его так, что одна из его сторон, образующих прямой угол угольника, располагалась вдоль стороны NР. Вторую сторону угольника, образующую прямой угол, располагаем так, что вершина M лежит вдоль этой стороны.
MNP из вершины M к стороне NP, берем чертежный угольник, прикладываем его так, что одна из его сторон, образующих прямой угол угольника, располагалась вдоль стороны NР. Вторую сторону угольника, образующую прямой угол, располагаем так, что вершина M лежит вдоль этой стороны.
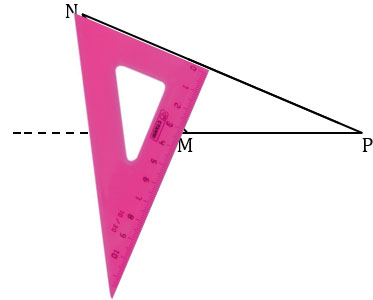
Далее из вершины M проводим прямую вдоль стороны угольника к стороне NP треугольника MNP.
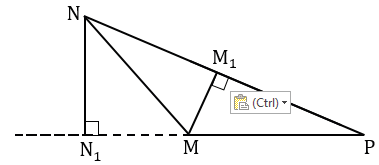
Точку пересечения проведенной прямой со стороной NР обозначаем M1. Получаем MM1 - высота треугольника MNP, проведенная к стороне NP.
Чтобы провести высоту 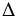 MNP из вершины P к стороне MN, берем чертежный угольник, прикладываем его так, что одна из его сторон, образующих прямой угол угольника, располагалась вдоль продолжения стороны МN. Вторую сторону угольника, образующую прямой угол, располагаем так, что вершина P лежит вдоль этой стороны.
MNP из вершины P к стороне MN, берем чертежный угольник, прикладываем его так, что одна из его сторон, образующих прямой угол угольника, располагалась вдоль продолжения стороны МN. Вторую сторону угольника, образующую прямой угол, располагаем так, что вершина P лежит вдоль этой стороны.
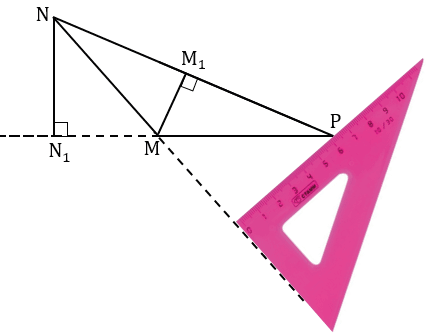
Далее из вершины P проводим прямую вдоль стороны угольника к продолжению стороны MN треугольника MNP.
Точку пересечения проведенной прямой с продолжением стороны МN обозначаем Р1. Получаем РР1 - высота треугольника MNP, проведенная к стороне МN.

Вернуться к содержанию учебника