Упражнение 286 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№286 учебника 2023-2025 (стр. 64):
Используя график функции (рис. 26), заполните таблицу, перечертив ее в тетрадь.
 |
-3 | -1,5 | -0,5 | 0 | 0,5 | 3,5 |
 |

Рис. 26
Укажите пять каких-либо значений аргумента, которым соответствуют положительные значения функции, и пять каких-либо значений аргумента, которым соответствуют отрицательные значения функции.
№286 учебника 2013-2022 (стр. 65):
Используя график функции (рис. 16), заполните таблицу, перечертив ее в тетрадь.
| \(x\) | -3 | -1,5 | -0,5 | 0 | 0,5 | 3,2 |
| \(y\) |
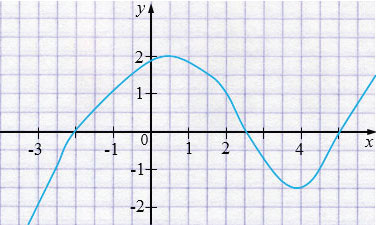
Рис. 16
Укажите пять значений аргумента, которым соответствуют положительные значения функции, и пять значений аргумента, которым соответствуют отрицательные значения функции.
Подсказка
№286 учебника 2023-2025 (стр. 64):
№286 учебника 2013-2022 (стр. 65):
Вспомните:
- Что называют функцией, аргументом.
- График функции.
- Перпендикулярные прямые.
Ответ
№286 учебника 2023-2025 (стр. 64):
 |
-3 | -1,5 | -0,5 | 0 | 0,5 | 3,5 |
 |
-2 | 0,5 | 1,5 | 1,8 | 2 | -1,3 |
 > 0 при
> 0 при  = -1,7; -0,8; 0,3; 1,5; 2.
= -1,7; -0,8; 0,3; 1,5; 2.
 < 0 при
< 0 при  = -2,8; -2,5; 3; 4; 4,5.
= -2,8; -2,5; 3; 4; 4,5.
Пояснения:
Чтобы определить значение функции  для значения аргумента
для значения аргумента  , равного -3, нужно через точку оси
, равного -3, нужно через точку оси  с абсциссой, равной -3, провести перпендикуляр к оси
с абсциссой, равной -3, провести перпендикуляр к оси  . Точка пересечения этого перпендикуляра с графиком функции имеет координаты (-3; -2). Значит, при
. Точка пересечения этого перпендикуляра с графиком функции имеет координаты (-3; -2). Значит, при  = -3 значение функции равно -2. Аналогично определяем значения функции
= -3 значение функции равно -2. Аналогично определяем значения функции  для остальных значений аргумента
для остальных значений аргумента  .
.

Функция принимает положительные значения там, где график расположен выше оси  , а отрицательные - так, где график расположен ниже оси
, а отрицательные - так, где график расположен ниже оси  .
.
№286 учебника 2013-2022 (стр. 65):
| \(x\) | -3 | -1,5 | -0,5 | 0 | 0,5 | 3,2 |
| \(y\) | -2 | 0,5 | 1,5 | 1,8 | 2 | -1 |
\(y\) > 0 при \(x\) = -1,7; -0,8; 0,3; 1,5; 2.
\(y\) < 0 при \(x\) = -2,8; -2,5; 3; 4; 4,5.
Пояснения:
Чтобы определить значение функции \(y\) для значения аргумента \(x\), равного -3, нужно через точку оси \(x\) с абсциссой, равной -3, провести перпендикуляр к оси \(x\). Точка пересечения этого перпендикуляра с графиком функции имеет координаты (-3; -2). Значит, при \(x\) = -3 значение функции равно -2. Аналогично определяем значения функции \(y\) для остальных значений аргумента \(x\).
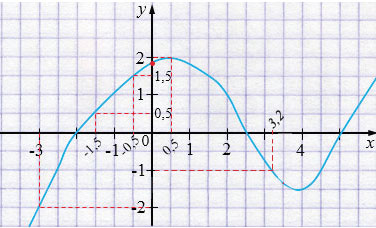
Функция принимает положительные значения там, где график расположен выше оси \(x\), а отрицательные - так, где график расположен ниже оси \(x\).
Вернуться к содержанию учебника