Задание 6.54 - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 2. Страница 107

АВС - треугольник с вершинами А(3; 5), В(3; -2), С(-5; -2).

а) Треугольник АВС прямоугольный, А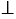В СВ.

б) длины сторон треугольника KMN пропорциональны длинам сторон треугольника АВС, так как

.

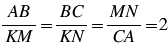Пояснения:

Чертим прямоугольную систему координат с единичным отрезком 1 клетка. Отмечаем в этой системе координат точки А(3; 5), В(3; -2), С(-5; -2).

Чтобы попасть в точку А с координатами (3; 5), нужно сначала пройти по оси 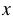от начала отсчета вправо на 3 единицы, а потом - на 5 единиц вверх.

Чтобы попасть в точку В с координатами (3; -2), нужно сначала пройти по оси 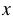от начала отсчета вправо на 3 единицы, а потом - на 2 единицы вниз.

Чтобы попасть в точку С с координатами (-5; -2), нужно сначала пройти по оси 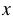от начала отсчета влево на 5 единиц, а потом - на 2 единицы вниз.

Соединив точки А, В и С получаем треугольник АВС.

а) Треугольник АВС прямоугольный, в нем перпендикулярны отрезки АВ и СВ, то есть А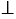В СВ.

б) С помощью линейки определяем середины K, М и N сторон АС, ВС и АВ соответственно (середина делит отрезок пополам) и, соединив точки K, М и N получаем треугольник KMN.

в) Пропорциональные отрезки — отрезки, для длин которых выполняется пропорция.Отношением отрезков AB и CD называется отношение их длин.

Каждая из сторон треугольника KMN в 2 раза меньше соответствующих сторон треугольника АВС (проверяем с помощью линейки). Тогда:

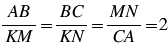, значит, длины сторон треугольника KMN пропорциональны длинам сторон треугольника АВС.